
题目列表(包括答案和解析)
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
已知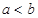 ,且
,且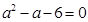 ,
,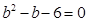 ,数列
,数列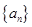 、
、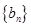 满足
满足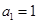 ,
,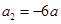 ,
, ,
,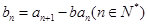 .
.
(1) 求证数列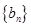 是等比数列;
是等比数列;
(2) (理科)求数列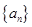 的通项公式
的通项公式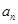 ;
;
(3) (理科)若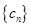 满足
满足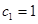 ,
,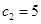 ,
,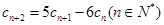 ,试用数学归纳法证明:
,试用数学归纳法证明:
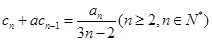 .
.
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分7分,第3小题满分5分.
在数列![]() (p为非零常数),则称数列
(p为非零常数),则称数列![]() 为“等差比”数列,p叫数列
为“等差比”数列,p叫数列![]() 的“公差比”.
的“公差比”.
已知数列![]() 满足
满足![]() ,判断该数列是否为等差比数列?
,判断该数列是否为等差比数列?
已知数列![]()
![]() 是等差比数列,且
是等差比数列,且![]() 公差比
公差比![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() ;
;
(3)记![]() 为(2)中数列
为(2)中数列![]() 的前n项的和,证明数列
的前n项的和,证明数列![]()
![]() 也是等差比数列,并求出公差比p的值.
也是等差比数列,并求出公差比p的值.
已知抛物线y2=8x的准线与双曲线![]() -
-![]() =1(a>0,b>0)相交于A,
=1(a>0,b>0)相交于A,![]() B两点,双曲线的一条渐近线方程是y=2
B两点,双曲线的一条渐近线方程是y=2![]() x,点F是抛物线的焦点,且△FAB是直角三角形,则双曲线的标准方程是( )
x,点F是抛物线的焦点,且△FAB是直角三角形,则双曲线的标准方程是( )
(A)![]() -
-![]() =1 (B)x2-
=1 (B)x2-![]() =1
=1
(C)![]() -
-![]() =1 (D)
=1 (D)![]() -y2=1
-y2=1
二、填空题(每小题6分,共18分)
(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分7分,第3小题满分5分.
已知各项都为正数的数列![]() ,其中
,其中![]() 的前n项的和.
的前n项的和.
(1)![]() ;
;
(2)已知p(![]() 2)是给定的某个正整数,数列
2)是给定的某个正整数,数列![]()
(![]() ),求
),求![]() ;
;
(3)化简![]() .
.
某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)。
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.
表1:
生产能力分组 |
|
|
|
|
|
人数 | 4 | 8 |
| 5 | 3 |
表2:
生产能力分组 |
|
|
|
|
人数 | 6 | y | 36 | 18 |
(i)先确定x,y,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)w.w.w.k.s.5.u.c.o.m

(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表)w.w.w.k.s.5.u.c.o.m
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com