
题目列表(包括答案和解析)
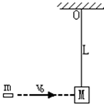 如图所示:质量为M=0.6kg的小沙箱,用长为L=1.60m的细线悬于空中某点,现用玩具手枪以v0=10m/s速度从左向右向沙箱发射质量m=0.2kg的子弹,假设沙箱每次在最低点时,就恰好有一颗子弹与沙箱迎面飞来,射入沙箱并留在其中,不计空气阻力,细线能承受的拉力足够大,子弹与沙箱的作用时间极短,取g=10m/s2,求解下列问题:
如图所示:质量为M=0.6kg的小沙箱,用长为L=1.60m的细线悬于空中某点,现用玩具手枪以v0=10m/s速度从左向右向沙箱发射质量m=0.2kg的子弹,假设沙箱每次在最低点时,就恰好有一颗子弹与沙箱迎面飞来,射入沙箱并留在其中,不计空气阻力,细线能承受的拉力足够大,子弹与沙箱的作用时间极短,取g=10m/s2,求解下列问题:| 2mv0 |
| M+2m |
| 2×0.2×10 |
| 0.6+2×0.2 |
解析 设冰壶质量为m,碰后中国队冰壶速度为vx,
由动量守恒定律得
mv0=mv+mvx
解得vx=0.1 m/s,故选项A正确.
答案 A
![]()

图甲 图乙
图7-19
①碰前m2静止,m1向右运动 ②碰后m2和m1都向右运动 ③由动量守恒定律可以算出m2=0.3 kg ④碰撞过程中系统损失了0.4 J的机械能
以上判断正确的是( )
A.①③ B.①②③ C.①②④ D.③④
1934年约里奥—居里夫妇用α粒子轰击静止的Al,发现了放射性磷P和另一种粒子,并因这一伟大发现而获得诺贝尔物理学奖.
(1)写出这个过程的核反应方程式.
(2)若该种粒子以初速度v0与一个静止的12C核发生碰撞,但没有发生核反应,该粒子碰后的速度大小为v1,运动方向与原运动方向相反,求碰撞后12C核的速度.
【解析】:(1)核反应方程式为:He+Al―→P+n
(2)设该种粒子的质量为m,则12C核的质量为12m.由动量守恒定律可得:mv0=m(-v1)+12mv2
解得:v2=
则碰撞后该种粒子运动方向与原粒子运动方向相同.
40 kg的女孩骑自行车带30 kg的男孩(如图18所示),行驶速度2.5 m/s.自行车行驶时,男孩要从车上下来.
(1)他知道如果直接跳下来,他可能会摔跤,为什么?
(2)计算男孩下车的瞬间,女孩和自行车的速度.
(3)计算自行车和两个孩子,在男孩下车前后整个系统的动能的值.如有不同,请解释.

【解析】:(1)如果直接跳下来,人具有和自行车相同的速度,脚着地后,脚的速度为零,由于惯性,上身继续向前倾斜,因此他可能会摔跤.所以他下来时用力往前推自行车,这样他下车时水平速度是0.
(2)男孩下车前后,对整体由动量守恒定律有:
(m1+m2+m3)v0=(m1+m2)v
v=4 m/s(m1表示女孩质量,m2表示自行车质量,m3表示男孩质量)
(3)男孩下车前系统的动能
Ek=(m1+m2+m3)v
=(40+10+30)×(2.5)2J
=250 J
男孩下车后系统的动能
Ek′=(m1+m2)v2=(40+10)×42J=400 J
男孩下车时用力向前推自行车,对系统做了正功,使系统的动能增加了150 J.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com