（本小题满分14分）如图，建立平面直角坐标系，轴在地平面上，轴垂直于地

平面，单位长度为1千米，某炮位于坐标原点．已知炮弹发射后的轨迹在方程表示的曲线上，其中与发射方向有关，炮的射程是指炮弹落地点的横坐标．

（1）求炮的最大射程；

（2）设在第一象限有一飞行物（忽略其大小），其飞行高度为3.2千米，试问它的横坐标不超过多少时，炮弹可以击中它？请说明理由．

.（本小题满分14分）

某校从参加高一年级期末考试的学生中抽出60名学生，将其成绩（均为整数）分成六段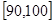，…后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：

（1）求第四小组的频率，并补全这个频率分布直方图；

（2）估计这次考试的及格率（60分及以上为及格）和平均分；

（3）用分层抽样的方法从成绩是80分以上（包括80分）的学生中抽取了6人进行试卷分析，再从这6个人中选2人作学习经验介绍发言，求选出的2人中至少有1人在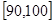的概率.

（本小题满分14分）

某慈善机构举办一次募捐演出，有一万人参加，每人一张门票，每张100元，在演出过程中穿插抽奖活动，第一轮抽奖从这一万张票根中随机抽取10张，其持有者获得价值1000元的奖品，并参加第二轮抽奖活动，第二轮抽奖由第一轮获奖者独立操作按钮，电脑随机产生两个数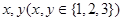，如果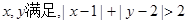则电脑显示“中奖”，抽奖者获得9000元奖金；否则若电脑显示“谢谢”，则不中奖。

（I）已知小曹在第一轮抽奖中被抽中，求小曹在第二轮抽奖中获奖的概率；

（II）若小叶参加了此次活动，求小叶参加此次活动收益的期望；

（III）若此次募捐除奖品和奖金外，不计其它支出，该机构想获得96万元的慈善款，问该慈善机构此次募捐是否能达到预期目标。

（本小题满分14分）如图，建立平面直角坐标系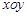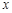，轴在地平面上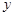，轴垂直于地
平面，单位长度为1千米，某炮位于坐标原点．已知炮弹发射后的轨迹在方程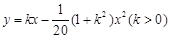表示的曲线上，其中与发射方向有关，炮的射程是指炮弹落地点的横坐标．
（1）求炮的最大射程；
（2）设在第一象限有一飞行物（忽略其大小），其飞行高度为3.2千米，试问它的横坐标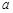不超过多少时，炮弹可以击中它？请说明理由．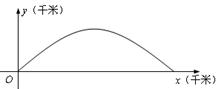

(本小题满分14分)

       小明参加一次智力问答比赛，比赛共设三关。第一、二关各有两个问题，两个问题全答对，可进入下一关。第三关有三个问题，只要答对其中两个问题，则闯关成功。每过一关可一次性获得价值分别为100、300、500元的奖励。小明对三关中每个问题回答正确的概率依次为、、，且每个问题回答正确与否相互独立。

   （1）求小明过第一关但未过第二关的概率；

   （2）用表示小明所获得奖品的价值，求的分布列和期望。