小丽是一位爱探索的学生，一个周末她在自己家门前的地上发现了一个不规则的封闭图形ABCD，她很想知道此图形的面积，于是她在封闭图形内划出了一个半径为1米的⊙O，在不远处向圈内掷石子，且记录如下：

掷石子次数 石子落在的区域	50次	150次	300次	400次	500次	800次
石子落在⊙O内（含⊙O上的次数）m	24	65	93	59	201	318
石子落在ABCD内，且在⊙O外的次数n	26	85	186	241	299	482

根据上表提供的信息，你能估计出图形ABCD的面积吗？若能，请写出估计的过程．

　　实践与探索课上，老师布置了这样一道题：

　　有100米长的篱笆材料，想围成一矩形露天仓库，要求面积不小于600平方米，在场地的北面有一堵长50米的旧墙．有人用这个篱笆围一个长40米，宽10米的矩形仓库，但面积只有400平方米，不合要求．现在请你设计矩形仓库的长和宽，使它符合要求．

　　经过同学们一天的实践与思考，老师收到了如下几种设计方案：

　　(1)如果设矩形的宽为x米，则用于长的篱笆为＝(50－x)米，这时面积S＝x(50－x)．

　　当S＝600时，由x(50－x)＝600，得x²－50x＋600＝0，解得x₁＝20，x₂＝30．

　　检验后知x＝20符合要求．

　　(2)根据在周长相等的条件下，正方形面积大于矩形面积，所以设计成正方形仓库，它的边长为x米，则4x＝100，x＝25．这时面积达到625米，当然符合要求．

　　(3)如果利用场地北面的那堵旧墙，取矩形的长与旧墙平行，设与墙垂直的矩形一边长为x米，则另一边为100－2x，如图．

　　因为旧墙长50米，所以100－2x≤50．即x≥25米．若S＝600平方米，则由x(100－2x)＝600，即x²－50x＋300＝0，解得x₁＝25＋，x₂＝25－．根据x≥25，舍去x₂＝25－．

　　所以，利用旧墙，取矩形垂直于旧墙一边长为25＋米(约43米)，另一边长约14米，符合要求．

　　(4)如果充分利用北面旧墙，即矩形一边是50米旧墙时，用100米篱笆围成矩形仓库，则矩形另一边长为25米，这时矩形面积为S＝50×25＝1250(平方米)．即面积可达1250平方米，符合设计要求．

还可以有其他一些符合要求的设计方案．请你试试看．

　　如图，某学习小组在探索“一点到等边三角形三边的距离与该等边三角形的高的关系”时，对话如下：

　　甲同学：我们先将要探索的问题具体化，(边说边画)等边△ABC，高为h．点P该在哪儿呢？

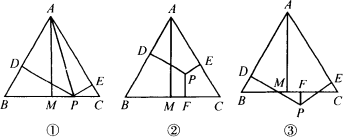
　　乙同学：我想，点P的位置就是分类讨论的关键．我们研究问题应该从特殊到一般．特殊的话，点P应该在等边△ABC的一边上，(边说边画，得图①)．只需连接AP，我就可以得到PD＋PE＝AM．

　　丙同学：结果要及时上升为规律．设点P到△ABC三边AB、AC、BC的距离分别为h₁、h₂、h₃．你的发现就可以归纳为h＝h₁＋h₂＋h₃．而点P在等边△ABC内部时(如图②)，这个结论也成立．

　　丁同学：如果点P在等边△ABC外部呢(如图③)？丙发现的“规律”好像有问题……

(1)请你证明丙同学的发现．

(2)丁同学发现了什么问题，提出你的猜想(不必证明)．