如图，AB为粗糙的长直斜面，动摩擦因数μ=0.4，与水平方向的夹角θ=37°，BC为光滑水平面，CDE为光滑曲面，B、C两接口处均光滑连接。D、E两点离水平地面的高度分别为h₁＝8.64m，h₂＝4m。一质量m＝0.20kg的滑块由斜面上某一点P从静止开始下滑，在斜面上始终受一水平向右恒力F=1N的作用，到达B点时立即撤去拉力F，从P点到达C点共经历t＝3s。已知PB与BC长度之和为32m。求：（sin37°＝0.6，cos37°＝0.8，g=10m/s²）

（1）滑块沿AB段运动时加速度a和所用时间t₁；

（2）若水平向右恒力F大小可调，则恒力F在何范围内可使滑块沿PB、BC运动越过曲面落地。某同学对第二问的解答如下：若要使滑块越过曲面落地，则离开曲面E点时的速度至少为0。从P点至E点列出动能定理。即可求得所需的最小恒力。请判断该同学的解答是否正确，并说明理由，若该同学解答错误则求出正确的恒力范围。

如图所示，将质量均为m厚度不计的两物块A、B用轻质弹簧相连接。第一次只用手托着B物块于H高度，A在弹簧弹力的作用下处于静止，现将弹簧锁定，此时弹簧的弹性势能为E_p，现由静止释放A、B，B物块刚要着地前瞬间将弹簧瞬间解除锁定（解除锁定无机构能损失），B物块着地后速度立即变为O，在随后的过程中B物块恰能离开地面但不继续上升。第二次用手拿着A、B两物块，使得弹簧竖直并处于原长状态，此时物块B离地面的距离也为H，然后由静止同时释放A、B，B物块着地后速度同样立即变为0。求：

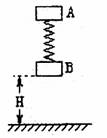
   （1）第二次释放A、B后，A上升至弹簧恢复原长时的速度v₁；

   （2）第二次释放A、B后，B刚要离地时A的速度v₂。

如图所示，将质量均为m厚度不计的两物块A、B用轻质弹簧相连接。第一次只用手托着B物块于H高度，A在弹簧弹力的作用下处于静止，现将弹簧锁定，此时弹簧的弹性势能为E_p，现由静止释放A、B，B物块刚要着地前瞬间将弹簧瞬间解除锁定（解除锁定无机构能损失），B物块着地后速度立即变为O，在随后的过程中B物块恰能离开地面但不继续上升。第二次用手拿着A、B两物块，使得弹簧竖直并处于原长状态，此时物块B离地面的距离也为H，然后由静止同时释放A、B，B物块着地后速度同样立即变为0。求：

　 （1）第二次释放A、B后，A上升至弹簧恢复原长时的速度v₁；

　 （2）第二次释放A、B后，B刚要离地时A的速度v₂。

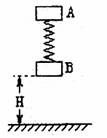
如图所示，一个半径为R的半球形的碗固定在桌面上，碗口水平，O点为其球心，碗的内表面及碗口是光滑的。一根轻质细线跨在碗口上，线的两端分别系有小球A和B，当它们处于平衡状态时，小球A与O点的连线与水平线的夹角为60°。

（1）求小球A与小球B的质量比m_A：m_B

（2）辨析题：现将A球质量改为2m、B球质量改为m，且开始时A球位于碗口C点，由静止沿碗下滑，当A球滑到碗底时，求两球的速率为多大？

某同学解法如下：当A球滑到碗底时，A球下降的高度为R，B球上升的高度为R，根据机械能守恒定律有：

  ① 且     ②

代入数据，解①、②两式即可求得两球的速率。   

你认为上述分析是否正确？如果你认为正确，请完成此题；如果你认为不正确，请指出错误，并给出正确的解答。

（3）在满足第（2）问中的条件下，求A球沿碗壁运动的最大位移是多少？

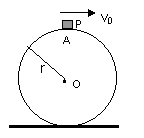
如图所示，横截面半径为r的圆柱体固定在水平地面上。一个质量为m的小滑块P从截面最高点A处以滑下。不计任何摩擦阻力。

（1）试对小滑块P从离开A点至落地的运动过程做出定性分析；

（2）计算小滑块P离开圆柱面时的瞬时速率和落地时的瞬时速率。

下面是某同学的一种解答：

（1） 小滑块在A点即离开柱面做平抛运动，直至落地。

（2） a、滑块P离开圆柱面时的瞬时速率为。

b、由： 得：

落地时的速率为　　

你认为该同学的解答是否正确？若正确，请说明理由。若不正确，请给出正确解答。