
题目列表(包括答案和解析)
设m,n是两条不同的直线,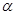 、
、 是两个不同的平面.则下列命题中正确的是( )
是两个不同的平面.则下列命题中正确的是( )
A.m⊥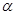 ,n ,n  ,m⊥n ,m⊥n 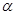 ⊥ ⊥ |
B.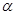 ⊥ ⊥ , ,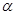 ∩ ∩ =m,n⊥m =m,n⊥m n⊥ n⊥ |
C.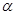 ⊥ ⊥ ,m⊥ ,m⊥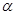 ,n∥ ,n∥  m⊥n m⊥n |
D.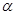 ∥ ∥ ,m⊥ ,m⊥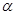 ,n∥ ,n∥  m⊥n m⊥n |
 的特征值及对应的特征向量.
的特征值及对应的特征向量.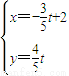 (t为参数).
(t为参数).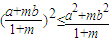 .
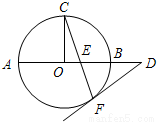
.
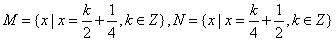 ,则
,则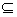 N
N 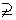 N
N 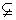 N
N 集合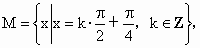
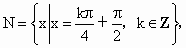 则
则
[ ]
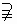 N
N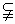 N
N
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
C
C
B
B
C
C
A
C
B
B
二、填空题
13..files/image229.gif) 14.
14. .files/image231.gif) 15.
15. .files/image233.gif) 16.___-1__
16.___-1__
三、解答题
17.解:1) .files/image235.gif)
=.files/image237.gif)
.files/image239.gif)
.files/image241.gif)
.files/image243.gif)
.files/image245.gif)
2).files/image247.gif)
.files/image249.gif) 或
或.files/image251.gif)
.files/image253.gif) 或
或.files/image255.gif) ,而
,而.files/image257.gif)
.files/image259.gif)
.files/image261.gif) ,
,.files/image263.gif)
18.解:(I)由题意:.files/image265.gif) 的取值为1,3,又
的取值为1,3,又.files/image267.gif)
.files/image269.gif)
|