（选修模块3-3）（12分）

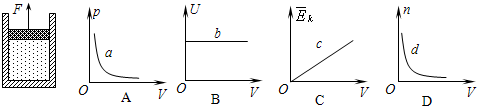
⑴如图，固定的导热气缸内用活塞密封一定质量的理想气体，气缸置于温度不变的环境中。现用力使活塞缓慢地向上移动，密闭气体的状态发生了变化。下列图象中p、V和U分别表示该气体的压强、体积和内能，表示该气体分子的平均动能，n表示单位体积内气体的分子数，a、d为双曲线，b、c为直线。能正确反映上述过程的是   ▲  

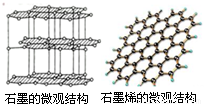
⑵2010年诺贝尔物理学奖授予安德烈·海姆和康斯坦丁·诺沃肖洛夫，以表彰他们在石墨烯材料方面的卓越研究。他们通过透明胶带对石墨进行反复的粘贴与撕开使得石墨片的厚度逐渐减小，最终寻找到了厚度只有0.34nm的石墨烯，是碳的二维结构。如图所示为石墨、石墨烯的微观结构，根据以上信息和已学知识判断，下列说法中正确的是   ▲    

A．石墨是晶体，石墨烯是非晶体

B．石墨是单质，石墨烯是化合物

C．石墨、石墨烯与金刚石都是晶体

D．他们是通过物理变化的方法获得石墨烯的

⑶为保证驾乘人员的安全，轿车中设有安全气囊。轿车在发生一定强度的碰撞时，利用叠氮化钠（NaN₃）爆炸产生气体(假设都是N₂)充入气囊。若氮气充入后安全气囊的容积V=56L，囊中氮气密度ρ=2.5kg/m³，已知氮气摩尔质量M=2.8×10^-2kg/mol，阿伏加德罗常数N_A=6.02×10²³mol^-1，试估算囊中氮气分子的总个数N（结果保留一位有效数字）。

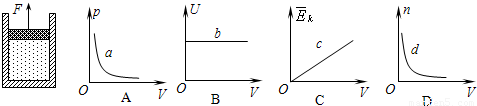
第七部分 热学

热学知识在奥赛中的要求不以深度见长，但知识点却非常地多（考纲中罗列的知识点几乎和整个力学——前五部分——的知识点数目相等）。而且，由于高考要求对热学的要求逐年降低（本届尤其低得“离谱”，连理想气体状态方程都没有了），这就客观上给奥赛培训增加了负担。因此，本部分只能采新授课的培训模式，将知识点和例题讲解及时地结合，争取让学员学一点，就领会一点、巩固一点，然后再层叠式地往前推进。

一、分子动理论

1、物质是由大量分子组成的（注意分子体积和分子所占据空间的区别）

对于分子（单原子分子）间距的计算，气体和液体可直接用，对固体，则与分子的空间排列（晶体的点阵）有关。

【例题1】如图6-1所示，食盐（N_aCl）的晶体是由钠离子（图中的白色圆点表示）和氯离子（图中的黑色圆点表示）组成的，离子键两两垂直且键长相等。已知食盐的摩尔质量为58.5×10^－3kg/mol，密度为2.2×10³kg/m³，阿伏加德罗常数为6.0×10²³mol^－1，求食盐晶体中两个距离最近的钠离子中心之间的距离。

【解说】题意所求即图中任意一个小立方块的变长（设为a）的倍，所以求a成为本题的焦点。

由于一摩尔的氯化钠含有N_A个氯化钠分子，事实上也含有2N_A个钠离子（或氯离子），所以每个钠离子占据空间为 v = 

而由图不难看出，一个离子占据的空间就是小立方体的体积a³ ，

即 a³ =  = ，最后，邻近钠离子之间的距离l = a

【答案】3.97×10^－10m 。

〖思考〗本题还有没有其它思路？

〖答案〗每个离子都被八个小立方体均分，故一个小立方体含有×8个离子 = 分子，所以…（此法普遍适用于空间点阵比较复杂的晶体结构。）

2、物质内的分子永不停息地作无规则运动

固体分子在平衡位置附近做微小振动（振幅数量级为0.1），少数可以脱离平衡位置运动。液体分子的运动则可以用“长时间的定居（振动）和短时间的迁移”来概括，这是由于液体分子间距较固体大的结果。气体分子基本“居无定所”，不停地迁移（常温下，速率数量级为10²m/s）。

无论是振动还是迁移，都具备两个特点：a、偶然无序（杂乱无章）和统计有序（分子数比率和速率对应一定的规律——如麦克斯韦速率分布函数，如图6-2所示）；b、剧烈程度和温度相关。

气体分子的三种速率。最可几速率v_P ：f(v) = （其中ΔN表示v到v +Δv内分子数，N表示分子总数）极大时的速率，v_P == ；平均速率：所有分子速率的算术平均值， ==；方均根速率：与分子平均动能密切相关的一个速率，==〔其中R为普适气体恒量，R = 8.31J/(mol.K)。k为玻耳兹曼常量，k =  = 1.38×10^－23J/K 〕

【例题2】证明理想气体的压强P = n，其中n为分子数密度，为气体分子平均动能。

【证明】气体的压强即单位面积容器壁所承受的分子的撞击力，这里可以设理想气体被封闭在一个边长为a的立方体容器中，如图6-3所示。

考查yoz平面的一个容器壁，P =            ①

设想在Δt时间内，有N_x个分子（设质量为m）沿x方向以恒定的速率v_x碰撞该容器壁，且碰后原速率弹回，则根据动量定理，容器壁承受的压力

 F ==                            ②

在气体的实际状况中，如何寻求N_x和v_x呢？

考查某一个分子的运动，设它的速度为v ，它沿x、y、z三个方向分解后，满足

v² =  +  + 

分子运动虽然是杂乱无章的，但仍具有“偶然无序和统计有序”的规律，即

 =  +  +  = 3                    ③

这就解决了v_x的问题。另外，从速度的分解不难理解，每一个分子都有机会均等的碰撞3个容器壁的可能。设Δt = ，则

 N_x = ·3N_总 = na³                         ④

注意，这里的是指有6个容器壁需要碰撞，而它们被碰的几率是均等的。

结合①②③④式不难证明题设结论。

〖思考〗此题有没有更简便的处理方法？

〖答案〗有。“命令”所有分子以相同的速率v沿+x、?x、+y、?y、+z、?z这6个方向运动（这样造成的宏观效果和“杂乱无章”地运动时是一样的），则 N_x =N_总 = na³ ；而且v_x = v

所以，P =  = ==nm = n

3、分子间存在相互作用力（注意分子斥力和气体分子碰撞作用力的区别），而且引力和斥力同时存在，宏观上感受到的是其合效果。

分子力是保守力，分子间距改变时，分子力做的功可以用分子势能的变化表示，分子势能E_P随分子间距的变化关系如图6-4所示。

分子势能和动能的总和称为物体的内能。

二、热现象和基本热力学定律

1、平衡态、状态参量

a、凡是与温度有关的现象均称为热现象，热学是研究热现象的科学。热学研究的对象都是有大量分子组成的宏观物体，通称为热力学系统（简称系统）。当系统的宏观性质不再随时间变化时，这样的状态称为平衡态。

b、系统处于平衡态时，所有宏观量都具有确定的值，这些确定的值称为状态参量（描述气体的状态参量就是P、V和T）。

c、热力学第零定律（温度存在定律）：若两个热力学系统中的任何一个系统都和第三个热力学系统处于热平衡状态，那么，这两个热力学系统也必定处于热平衡。这个定律反映出：处在同一热平衡状态的所有的热力学系统都具有一个共同的宏观特征，这一特征是由这些互为热平衡系统的状态所决定的一个数值相等的状态函数，这个状态函数被定义为温度。

2、温度

a、温度即物体的冷热程度，温度的数值表示法称为温标。典型的温标有摄氏温标t、华氏温标F（F = t + 32）和热力学温标T（T = t + 273.15）。

b、（理想）气体温度的微观解释： = kT （i为分子的自由度 = 平动自由度t + 转动自由度r + 振动自由度s 。对单原子分子i = 3 ，“刚性”〈忽略振动，s = 0，但r = 2〉双原子分子i = 5 。对于三个或三个以上的多原子分子，i = 6 。能量按自由度是均分的），所以说温度是物质分子平均动能的标志。

c、热力学第三定律：热力学零度不可能达到。（结合分子动理论的观点2和温度的微观解释很好理解。）

3、热力学过程

a、热传递。热传递有三种方式：传导（对长L、横截面积S的柱体，Q = KSΔ