
题目列表(包括答案和解析)
已知函数f(x)= ,
, 为常数。
为常数。
(I)当 =1时,求f(x)的单调区间;
=1时,求f(x)的单调区间;
(II)若函数f(x)在区间[1,2]上为单调函数,求 的取值范围。
的取值范围。
【解析】本试题主要考查了导数在研究函数中的运用。第一问中,利用当a=1时,f(x)= ,则f(x)的定义域是
,则f(x)的定义域是 然后求导,
然后求导, ,得到由
,得到由 ,得0<x<1;由
,得0<x<1;由 ,得x>1;得到单调区间。第二问函数f(x)在区间[1,2]上为单调函数,则
,得x>1;得到单调区间。第二问函数f(x)在区间[1,2]上为单调函数,则 或
或 在区间[1,2]上恒成立,即即
在区间[1,2]上恒成立,即即 ,或
,或 在区间[1,2]上恒成立,解得a的范围。
在区间[1,2]上恒成立,解得a的范围。
(1)当a=1时,f(x)= ,则f(x)的定义域是
,则f(x)的定义域是
 。
。
由 ,得0<x<1;由
,得0<x<1;由 ,得x>1;
,得x>1;
∴f(x)在(0,1)上是增函数,在(1, 上是减函数。……………6分
上是减函数。……………6分
(2) 。若函数f(x)在区间[1,2]上为单调函数,
。若函数f(x)在区间[1,2]上为单调函数,
则 或
或 在区间[1,2]上恒成立。∴
在区间[1,2]上恒成立。∴ ,或
,或 在区间[1,2]上恒成立。即
在区间[1,2]上恒成立。即 ,或
,或 在区间[1,2]上恒成立。
在区间[1,2]上恒成立。
又h(x)= 在区间[1,2]上是增函数。h(x)max=(2)=
在区间[1,2]上是增函数。h(x)max=(2)= ,h(x)min=h(1)=3
,h(x)min=h(1)=3
即
 ,或
,或 。 ∴
。 ∴
 ,或
,或 。
。
已知函数![]()
(I)化简![]() 的最小正周期;
的最小正周期;
(II)当![]() 的值域。
的值域。
(本小题满分14分)
|
(I)当![]() 的值域;
的值域;
(II)对于任意![]() 成立,求实数
成立,求实数![]() 的取值范围。
的取值范围。
(本小题满分12分)已知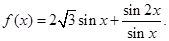
(I)求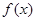 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。
(II)在三角形ABC中a、b、c分别是角A、B、C所对的边,对定义域内任意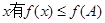 ,且b=1,c=2,求a的值。
,且b=1,c=2,求a的值。
(本小题满分12分)已知
(I)求 的最大值,及当取最大值时x的取值集合。
的最大值,及当取最大值时x的取值集合。
(II)在三角形ABC中a、b、c分别是角A、B、C所对的边,对定义域内任意 ,且b=1,c=2,求a的值。
,且b=1,c=2,求a的值。
一、选择题(本大题共10小题,每小题5分,共50分)
1―5 ADAAC 6―10 CBCDB
二、填空题(本大题共7小题,每小题4分,共28分)
11..files/image142.gif) 12.64 13.
12.64 13..files/image144.gif) 14.1 15.50 16.5 17.2
14.1 15.50 16.5 17.2
三、解答题(本大题共5小题,共72分。解答应写出文字说明、证明过程或演算过程)
18.(本小题满分14分)
解:(I).files/image146.gif) ………………2分
………………2分
.files/image148.gif) ………………4分
………………4分
.files/image150.gif) ………………6分
………………6分
故.files/image152.gif) ………………7分
………………7分
(II)当.files/image154.gif) ………………9分
………………9分
故.files/image156.gif) ………………12分
………………12分
故函数.files/image158.gif) 的值域为[―1,2]。
………………14分
的值域为[―1,2]。
………………14分
|