
题目列表(包括答案和解析)
给出问题:F1、F2是双曲线![]() -
-![]() =1的焦点,点P在双曲线上
=1的焦点,点P在双曲线上![]() 若点P到焦点F1的距离等于9,求点P到焦点F2的距离
若点P到焦点F1的距离等于9,求点P到焦点F2的距离![]() 某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17
某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17![]()
该学生的解答是否正确?若正确,请将他的解题依据填在下面横线上;若不正确,将正确结果填在下面横线上![]()
____________
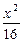 -
-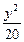 =1的焦点,点P在双曲线上
=1的焦点,点P在双曲线上 若点P到焦点F1的距离等于9,求点P到焦点F2的距离
若点P到焦点F1的距离等于9,求点P到焦点F2的距离 某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17
某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17

该学生的解答是否正确?若正确,请将他的解题依据填在下面空格内,若不正确,将正确结果填在下面空格内.
12.给出问题:F1、F2是双曲线![]() -
-![]() =1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P
=1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P
到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
该学生的解答是否正确?若正确,请将他的解题依据填在下面空格内,若不正确,将正确结果填在下面横线上.
______________________________________________________________
给出问题:F1、F2是双曲线 -
-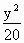 =1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
=1的焦点,点P在双曲线上.若点P到焦点F1的距离等于9,求点P到焦点F2的距离.某学生的解答如下:双曲线的实轴长为8,由||PF1|-|PF2||=8,即|9-|PF2||=8,得|PF2|=1或17.
该学生的解答是否正确?若正确,请将他的解题依据填在下面空格内;若不正确,将正确结果填在下面空格内.
________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com