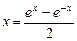在技术工程上常用双曲正弦函数sh和双曲余弦函数ch,而这两个函数与我们学过的正弦函数和余弦函数有类似的性质,如关于正、余弦函数有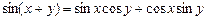,而双曲正、余弦函数也满足sh（x+y）=shxchy+chxshy,请你运用类比的方法另外写一个双曲正、余弦函数满足的关系式__________________．

(2006重庆课改，25)问题背景　　某课外学习小组在一次学习研讨中，得到了如下两个命题：

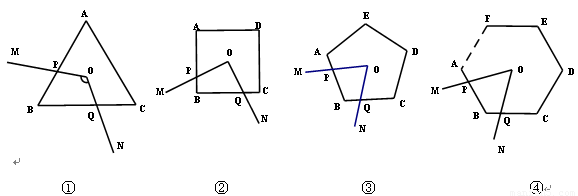
①如图1，在正三角形ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON=60°，则BM=CN；

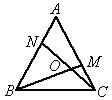
图1

②如图2，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON=90°，则BM=CN．

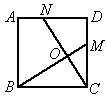
图2

然后运用类比的思想提出了如下命题：

③如图3，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON=108°，则BM=CN．

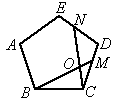
图3

任务要求

(1)请你从①，②，③三个命题中选择一个进行证明；(说明：选①做对的得4分，选②做对的得3分，选③做对的得5分)

(2)请你继续完成下面的探索：

①如图4，在正n(n≥3)边形ABCDEF…中，M、N分别是CD、DE上的点，BM与CN相交于点O，问当∠BON等于多少度时，结论BM=CN成立？(不要求证明)

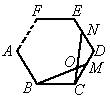
图4

②如图5，在正五边形ABCDE中，M、N分别是DE、AE上的点，BM与CN相交于点O，若∠BON=108°时，请问结论BM=CN是否还成立？若成立，请给予证明；若不成立，请说明理由．

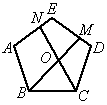
图5

(1)我选________．

证明：

问题背景 某课外学习小组在一次学习研讨中，得到如下两个命题：

① 如图1，在正三角形ABC中，M、N分别是AC、AB上的点，BM与CN相交于点O，若∠BON = 60°，则BM = CN.

② 如图2，在正方形ABCD中，M、N分别是CD、AD上的点，BM与CN相交于点O，若∠BON = 90°,则BM = CN.

然后运用类比的思想提出了如下的命题：

③ 如图3，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若∠BON = 108°，则BM = CN.

任务要求

(1）请你从①、②、③三个命题中选择一个进行证明；（说明：选①做对的得4分，选②做对的得3分，选③做对的得5分）

(2）请你继续完成下面的探索：

① 如图4，在正n（n≥3）边形ABCDEF…中，M、N分别是CD、DE上的点，BM与CN相交于点O，问当∠BON等于多少度时，结论BM = CN成立？（不要求证明）

② 如图5，在五边形ABCDE中，M、N分别是DE、AE上的点，BM与CN相交于点O，当∠BON = 108°时，请问结论BM = CN是否还成立？若成立，请给予证明；若不成立，请说明理由.

(1）我选 .

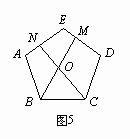
证明：

　

画图说明题：

（1）借助手中的三角板，画∠AOB＝90°

（2）在∠AOB的内部任画出一条射线OM

（3）画∠AOM的平分线OC，∠BOM的平分线OD

（4）用量角器量得∠COD＝      　　　　

试用说理的方法说明你所得结果的正确性.

 

问题背景  某课外学习小组在一次学习研讨中，得到如下两个命题：

①如图1，O是正三角形ABC的中心，∠MON分别与AB、BC交于点P,Q，若∠MON = 120°，则四边形OPBQ的面积等于三角形ABC面积的三分之一.

②如图2，O是正方形ABCD的中心，∠MON分别与AB、BC交于点P,Q，若∠MON = 90°，则四边形OPBQ的面积等于正方形ABCD面积的四分之一.

然后运用类比的思想提出了如下的命题：

③如图3，O是正五边形ABCDE的中心，∠MON分别与AB、BC交于点P,Q，若∠MON = 72°，则四边形OPBQ的面积等于五边形ABCDE面积的五分之一.

任务要求 

（1）请你从①、②、③三个命题中选择一个进行证明；（说明：选①做对的得5分，选②做对的得4分，选③做对的得6分）

（2）请你继续完成下面的探索：

如图④，在正n（n≥3）边形ABCDEF…中，O是中心,∠MON分别与AB、BC交于点P,Q，若∠MON 等于多少度时，则四边形OPBQ的面积等于正n边形ABCDE…面积的n分之一？（不要求证明）

解：（1）我选           .