对于各项均为整数的数列{a_n}，如果满足a_i+i（i=1，2，3，…）为完全平方数，则称数列{a_n}具有“P性质”；
不论数列{a_n}是否具有“P性质”，如果存在与{a_n}不是同一数列的{b_n}，且{b_n}同时满足下面两个条件：①b₁，b₂，b₃，…，b_n是a₁，a₂，a₃，…，a_n的一个排列；②数列{b_n}具有“P性质”，则称数列{a_n}具有“变换P性质”．
（Ⅰ）设数列{a_n}的前n项和Sn=

n

3

(n2-1)，证明数列{a_n}具有“P性质”；
（Ⅱ）试判断数列1，2，3，4，5和数列1，2，3，…，11是否具有“变换P性质”，具有此性质的数列请写出相应的数列{b_n}，不具此性质的说明理由；
（Ⅲ）对于有限项数列A：1，2，3，…，n，某人已经验证当n∈[12，m²]（m≥5）时，数列A具有“变换P性质”，试证明：当n∈[m²+1，（m+1）²]时，数列A也具有“变换P性质”．

对于各项均为整数的数列，如果（=1，2，3，…）为完全平方数，则称数

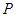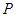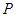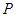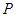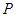列具有“性质”．不论数列是否具有“性质”，如果存在与不是同一数列的，且同时满足下面两个条件：①是的一个排列；②数列具有“性质”，则称数列具有“变换性质”．下面三个数列：①数列的前项和；②数列1，2，3，4，5；③1，2，3，…，11．具有“性质”的为         ；具有“变换性质”的为         ．

 

（本小题满分13分）

    对于各项均为整数的数列，如果(=1，2，3，…)为完全平方数，则称数

列具有“性质”。

    不论数列是否具有“性质”，如果存在与不是同一数列的，且同

时满足下面两个条件：①是的一个排列；②数列具有“性质”，则称数列具有“变换性质”。

（I）设数列的前项和，证明数列具有“性质”；

（II）试判断数列1，2，3，4，5和数列1，2，3，…，11是否具有“变换性质”，具有此性质的数列请写出相应的数列，不具此性质的说明理由；

（III）对于有限项数列：1，2，3，…，，某人已经验证当时，

数列具有“变换性质”，试证明：当”时，数列也具有“变换性质”。