
题目列表(包括答案和解析)
(8分)全国著名发明家邹德俊发明了一种“吸盘式”挂衣钩,如图所示,将它紧压在平整、清洁的竖直瓷砖墙面上时,可挂上衣帽等物品,假设挂衣钩的吸盘压紧时,吸盘的圆面可以跟墙面完全接触。已知吸盘与墙面间的动摩擦因数为0.5,吸盘的圆面直径为![]() ,那么这种挂钩最多能挂多重的物体?(大气压强 P0=1.0×105Pa,设吸盘与墙面间的最大静摩擦力等于滑动摩擦力)
,那么这种挂钩最多能挂多重的物体?(大气压强 P0=1.0×105Pa,设吸盘与墙面间的最大静摩擦力等于滑动摩擦力)

全国著名发明家邹德俊发明了一种“吸盘式”挂衣钩,如图所示,将它紧压在平整、清洁的竖直瓷砖墙面上时,可挂上衣帽等物品.如果挂衣钩的吸盘压紧时,它的圆面直径为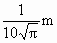 ,吸盘圆面压在墙上的
,吸盘圆面压在墙上的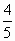 的面积跟墙面完全接触,中间
的面积跟墙面完全接触,中间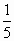 未接触部分间无空气.已知吸盘与墙角面间的动摩擦因数为0.5,则这种挂钩最多能挂多重的物体?(大气压强
未接触部分间无空气.已知吸盘与墙角面间的动摩擦因数为0.5,则这种挂钩最多能挂多重的物体?(大气压强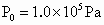 )
)
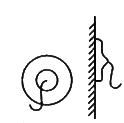
全国著名发明家邹德俊发明了一种“吸盘式”挂衣钩,如图所示,将它紧压在平整、清洁的竖直瓷砖墙面上时,可挂上衣帽等物品.如果挂衣钩的吸盘压紧时,它的圆面直径为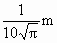 ,吸盘圆面压在墙上的
,吸盘圆面压在墙上的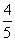 的面积跟墙面完全接触,中间
的面积跟墙面完全接触,中间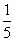 未接触部分间无空气.已知吸盘与墙角面间的动摩擦因数为0.5,则这种挂钩最多能挂多重的物体?(大气压强
未接触部分间无空气.已知吸盘与墙角面间的动摩擦因数为0.5,则这种挂钩最多能挂多重的物体?(大气压强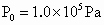 )
)
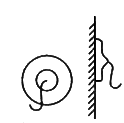
全国著名发明家邹德俊发明了一种“吸盘式”挂衣钩,如图所示,将它紧压在平整、清洁的竖直瓷砖墙面上时,可挂上衣帽等物品.如果挂衣钩的吸盘压紧时,它的圆面直径为![]() m,吸盘圆面压在墙上的
m,吸盘圆面压在墙上的![]() 的面积跟墙面完全接触,中间
的面积跟墙面完全接触,中间![]() 未接触部分间无空气.已知吸盘与墙面间的动摩擦因数为0.5,则这种挂钩最多能挂多重的物体?(大气压强P0=1.0×105 Pa)
未接触部分间无空气.已知吸盘与墙面间的动摩擦因数为0.5,则这种挂钩最多能挂多重的物体?(大气压强P0=1.0×105 Pa)

 全国著名发明家邹德俊,发明了一种“吸盘式”挂衣钩,如图所示.将它紧压在平整、清洁的竖直瓷砖墙面上时,可挂上衣帽等物品.如果挂衣钩的吸盘压紧时,它的圆面直径为
全国著名发明家邹德俊,发明了一种“吸盘式”挂衣钩,如图所示.将它紧压在平整、清洁的竖直瓷砖墙面上时,可挂上衣帽等物品.如果挂衣钩的吸盘压紧时,它的圆面直径为| 1 | ||
10
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com