练习册

  • 练习册
  • 试题
    双曲线的中心为原点.焦点在轴上.两条渐近线分别为l1.l2. 经过右焦点垂直于l1的直线分别交l1.l2于两点．已知成等差数 列.且与同向． (Ⅰ)求双曲线的离心率, (Ⅱ)设被双曲线所截得的线段的长为4.求双曲线的方程． 解:(Ⅰ)设.. 由勾股定理可得: 得:.. 由倍角公式.解得,则离心率． (Ⅱ)过直线方程为,与双曲线方程联立 将.代入.化简有 将数值代入.有,解得 故所求的双曲线方程为. 【查看更多】

     

    题目列表(包括答案和解析)

    （08年全国卷2理）从20名男同学，10名女同学中任选3名参加体能测试，则选到的3名同学中既有男同学又有女同学的概率为

    A．    B.      C.      D.

    查看答案和解析>>

    （08年全国卷2理）设曲线在点（0，1）处的切线与直线垂直，则a=          .

    查看答案和解析>>

    （08年全国卷2理）设a，b∈R且b≠0，若复数是实数，则

    A．   B.    C.    D. 

    查看答案和解析>>

    (2008全国高考卷Ⅱ,13)设向量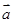＝(1,2), 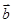＝(2,3).若向量λ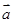+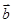与向量＝(-4,-7)共线,则λ＝_____________.

     

    查看答案和解析>>

    （08年全国卷2理）已知F为抛物线C：的焦点，过F且斜率为1的直线交C于A、B两点.设.则与的比值等于                     .

    查看答案和解析>>


    同步练习册答案