
题目列表(包括答案和解析)
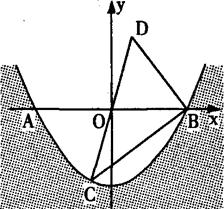
 (2013•哈尔滨)某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2-4.
(2013•哈尔滨)某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2-4.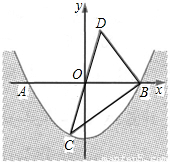 某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2-4.
某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2-4. 如图所示,已知在直角梯形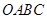 中,
中,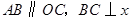 轴于点
轴于点 .动点
.动点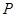 从
从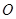 点出发,沿
点出发,沿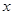 轴正方向以每秒1个单位长度的速度移动.过
轴正方向以每秒1个单位长度的速度移动.过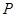 点作
点作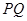 垂直于直线
垂直于直线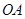 ,垂足为
,垂足为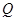 .设
.设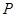 点移动的时间为
点移动的时间为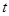 秒(
秒(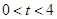 ),
),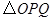 与直角梯形
与直角梯形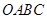 重叠部分的面积为
重叠部分的面积为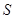 .
.

(1)求经过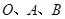 三点的抛物线解析式;
三点的抛物线解析式;
(2)将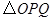 绕着点
绕着点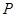 顺时针旋转
顺时针旋转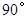 ,是否存在
,是否存在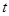 ,使得
,使得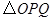 的顶点
的顶点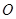 或
或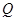 在抛物线上?若存在,直接写出
在抛物线上?若存在,直接写出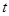 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)求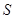 与
与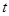 的函数关系式.
的函数关系式.
【解析】(1)设抛物线解析式为y=ax2+bx,把已知坐标代入求出抛物线的解析式(2)根据旋转的性质,代入解析式,判断是否存在(3)求出S的面积,根据t的取值不同分三种情况讨论S与t的函数关系式
 某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2-4.
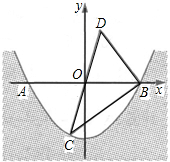
某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2-4.某水渠的横截面呈抛物线形,水面的宽为AB(单位:米)。现以AB所在直线为x轴.以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米。设抛物线解析式为y=ax2-4.
(1)求a的值;
(2)点C(一1,m)是抛物线上一点,点C关于原点0的对称点为点D,连接CD、BC、BD,求ABCD的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com