已知，如图，在平面直角坐标系中，点A坐标为(－2，0)，点B坐标为 （0，2 ），点E为线段AB上的动点(点E不与点A，B重合)，以E为顶点作∠OET=45°，射线ET交线段OB于点F，C为y轴正半轴上一点，且OC=AB，抛物线y=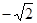x²+mx+n的图象经过A，C两点.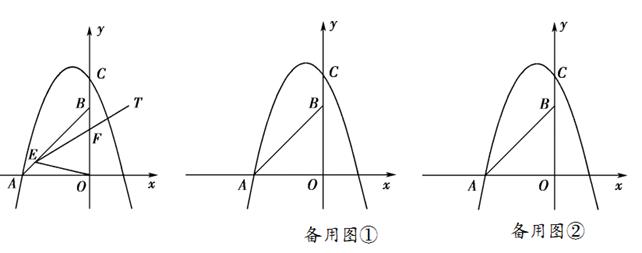

（1） 求此抛物线的函数表达式；
（2） 求证：∠BEF=∠AOE；
（3） 当△EOF为等腰三角形时，求此时点E的坐标；
（4） 在（3）的条件下，当直线EF交x轴于点D，P为（1） 中抛物线上一动点，直线PE交x轴于点G，在直线EF上方的抛物线上是否存在一点P，使得△EPF的面积是△EDG面积的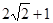（） 倍.若存在，请直接写出点P的坐标；若不存在，请说明理由．
温馨提示：考生可以根据题意，在备用图中补充图形，以便作答.

已知，如图，在平面直角坐标系中，点A坐标为(－2，0)，点B坐标为 （0，2 ），点E为线段AB上的动点(点E不与点A，B重合)，以E为顶点作∠OET=45°，射线ET交线段OB于点F，C为y轴正半轴上一点，且OC=AB，抛物线y=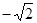x²+mx+n的图象经过A，C两点.

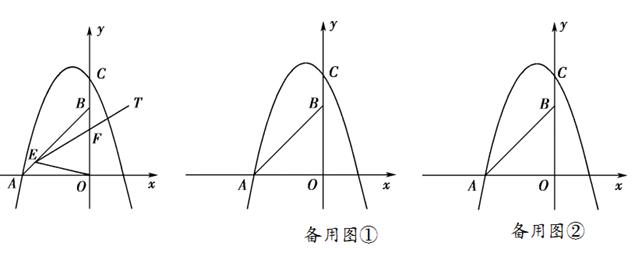
（1） 求此抛物线的函数表达式；

（2） 求证：∠BEF=∠AOE；

（3） 当△EOF为等腰三角形时，求此时点E的坐标；

（4） 在（3）的条件下，当直线EF交x轴于点D，P为（1） 中抛物线上一动点，直线PE交x轴于点G，在直线EF上方的抛物线上是否存在一点P，使得△EPF的面积是△EDG面积的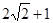（） 倍.若存在，请直接写出点P的坐标；若不存在，请说明理由．

温馨提示：考生可以根据题意，在备用图中补充图形，以便作答.

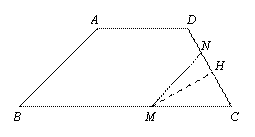
解：（1）由题意知，当、运动到秒时，如图①，过作交于点，则四边形是平行四边形．

∵，．

∴．

∴．

∴ ．解得．  5分

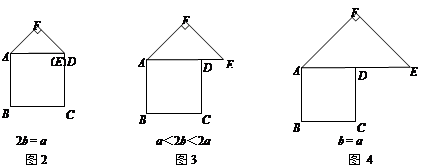
（2）分三种情况讨论：

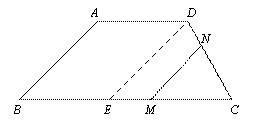
① 当时，如图②作交于，则有即．

∵，

∴，

∴，

解得． 6分

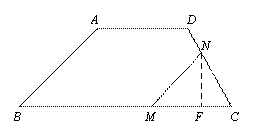
② 当时，如图③，过作于H．

则，

∴．

∴．7分

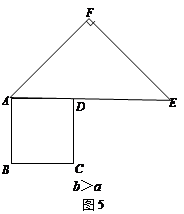
③ 当时，如图④．

则．

．      -------------------------------------8分

综上所述，当、或时，为等腰三角形．