22、某超市为了促销,推出两种促销方式:
方式①:所有商品实行7.5折销售;
方式②:一次购物满200元送60元现金.
试解答下列问题:
(1)杨师傅要购买标价为628元和788元的商品各一件,现有四种购买方案:
方案一:628元和788元的商品均按促销方式①购买;
方案二:628元的商品按促销方式①购买,788元的商品按促销方式②购买;
方案三:628元的商品按促销方式②购买,788元的商品按促销方式①购买;
方案四:628元和788元的商品均按促销方式②购买.
请你帮杨师傅计算出四种购买方案所付金额,并给杨师傅提出省钱的购买方案.
(2)计算下表中标价在600元到800元之间商品的付款金额:
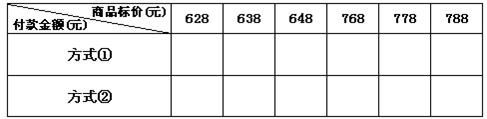
根据上表计算的结果,你能总结出商品的购买规律吗?