
题目列表(包括答案和解析)
 (2013•镇江)通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=
(2013•镇江)通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数y=| k |
| x+2 |
| k |
| x |
| 4 |
| x |
| 4 |
| x |
| 4 |
| x-1 |
通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x﹣1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数 的图象是由反比例函数
的图象是由反比例函数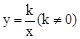 的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
如图,已知反比例函数 的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
(1)写出点B的坐标,并求a的值;
(2)将函数 的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).
的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).
①求n的值;
②分别写出平移后的两个图象C′和l′对应的函数关系式;
③直接写出不等式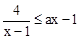 的解集.
的解集.

 通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数
通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数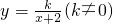 的图象是由反比例函数
的图象是由反比例函数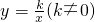 的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
的图象向左平移2个单位长度得到.灵活运用这一知识解决问题. 的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B. 的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).
的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).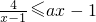 的解集.
的解集. 通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数
通过对苏科版八(下)教材一道习题的探索研究,我们知道:一次函数y=x-1的图象可以由正比例函数y=x的图象向右平移1个单位长度得到类似的,函数 的图象是由反比例函数
的图象是由反比例函数 的图象向左平移2个单位长度得到.灵活运用这一知识解决问题.
的图象向左平移2个单位长度得到.灵活运用这一知识解决问题. 的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B.
的图象C与正比例函数y=ax(a≠0)的图象l相交于点A(2,2)和点B. 的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4).
的图象和直线AB同时向右平移n(n>0)个单位长度,得到的图象分别记为C′和l′,已知图象C′经过点M(2,4). 的解集.
的解集.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com