先阅读下列材料,再解答后面的问题.
材料:密码学是一门很神秘、很有趣的学问,在密码学中,直接可以看到的信息称为明码,加密后的信息称为密码,任何密码只要找到了明码与密码的对应关系--密钥,就可以破译它.
密码学与数学是有关系的.为此,八年一班数学兴趣小组经过研究实验,用所学的一次函数知识制作了一种密钥的编制程序.他们首先设计了一个“字母--明码对照表”:
| 字母 |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
| 明码 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| 字母 |
N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
| 明码 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
13 |
24 |
25 |
26 |
例如,以y=3x+13为密钥,将“自信”二字进行加密转换后得到下表:
| 汉字 |
自 |
信 |
| 拼音 |
Z |
I |
X |
I |
N |
| 明码:x |
26 |
9 |
24 |
9 |
14 |
密钥:y= |
| 密码:y |
91 |
40 |
|
|
|
因此,“自”字加密转换后的结果是“9140”.
问题:
(1)请你求出当密钥为y=3x+13时,“信”字经加密转换后的结果;
(2)为了提高密码的保密程度,需要频繁地更换密钥.若“自信”二字用新的密钥加密转换后得到下表:
| 汉字 |
自 |
信 |
| 拼音 |
Z |
I |
X |
I |
N |
| 明码:x |
26 |
9 |
24 |
9 |
14 |
密钥:y=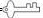 |
| 密码:y |
70 |
36 |
|
|
|
请求出这个新的密钥,并直接写出“信”字用新的密钥加密转换后的结果.


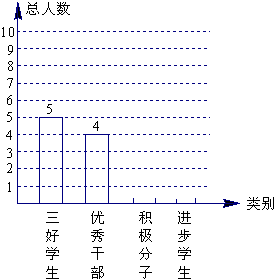 (2011•沙坪坝区模拟)某中学初三年级一、二班优秀学生的情况分布如表:
(2011•沙坪坝区模拟)某中学初三年级一、二班优秀学生的情况分布如表: