
题目列表(包括答案和解析)
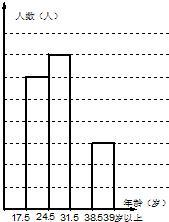 18、广州市2010亚运会将招募59000名志愿者.为了解志愿者的年龄结构,从中随机抽取1000名志愿者,年龄从低到高按18~24岁、25~31岁、32~38岁、39岁以上,分成四个年龄段进行统计(志愿者招募最小年龄为18岁,且年龄均为整数),整理后绘出如图所示的各年龄段的频数分布直方图的一部分,已知18~24岁、25~31岁和39岁以上这三个年龄段的频率分别为0.30、0.35和0.15.
18、广州市2010亚运会将招募59000名志愿者.为了解志愿者的年龄结构,从中随机抽取1000名志愿者,年龄从低到高按18~24岁、25~31岁、32~38岁、39岁以上,分成四个年龄段进行统计(志愿者招募最小年龄为18岁,且年龄均为整数),整理后绘出如图所示的各年龄段的频数分布直方图的一部分,已知18~24岁、25~31岁和39岁以上这三个年龄段的频率分别为0.30、0.35和0.15.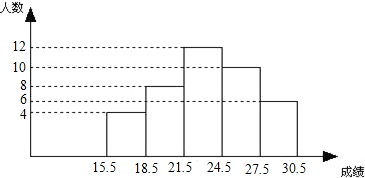


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com