练习册

  • 练习册
  • 试题
    向量的运算 (1)向量加法设.则+==. 向量加法的“三角形法则 与“平行四边形法则 (1)用平行四边形法则时.两个已知向量是要共始点的.和向量是始点与已知向量的始点重合的那条对角线.而差向量是另一条对角线.方向是从减向量指向被减向量. (2) 三角形法则的特点是“首尾相接 .由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和,差向量是从减向量的终点指向被减向量的终点. 当两个向量的起点公共时.用平行四边形法则,当两向量是首尾连接时.用三角形法则. 向量加法的三角形法则可推广至多个向量相加: .但这时必须“首尾相连 . (2)向量的减法 作图法:可以表示为从的终点指向的终点的向量(.有共同起点). 【查看更多】

     

    题目列表(包括答案和解析)

    若规定向量的运算符号“?”的运算规则为：
    a
    ?
    b
    =
    a
    •
    b
    -|
    a
    ||
    b
    |
    		1-(
    a
    •
    b
    |
    a
    |•|
    b
    |
    )    2
    （其中
    a
    •
    b
    表示向量
    a
    与
    b
    的数量积），若|
    a
    |=2，|
    b
    |=3，则
    a
    ?
    b
    的最小值为（　　）

    查看答案和解析>>

    （2012•闵行区一模）对于
    m
    =（x1，y1），
    n
    =（x2，y2），规定向量的“*”运算为：
    m
    *
    n
    =（x1x2，y1y2）．若
    a
    =（x，1），
    b
    =（-1，x），
    e1
    =（1，0），
    e2
    =（0，1）．解不等式
    (
    a
    * 
    b
    )•
    e1
    +1 
    (
    a
    *
    b
    ) •
    e2
    +1
    ＞1    ．

    查看答案和解析>>

    下面几种推理是类比推理的是（     ）

      A．两条直线平行，同旁内角互补，如果和是两条平行直线的同旁内角，则

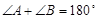
      B．由平面向量的运算性质，推测空间向量的运算性质

      C．某校高二级有20个班，1班有51位团员，2班有53位团员，3班有52位团员，由此可以推测各班都超过50位团员

      D．一切偶数都能被2整除，是偶数，所以能被2整除

     

    查看答案和解析>>

    （本题满分16分，第（1）小题6分，第（2）小题10分）

    设， 定义一种向量的运算：，点P（x，y）在函数的图像上运动，点Q在的图像上运动，且满足（其中O为坐标原点）

        （1）求函数f（x）的解析式；

        （2）若函数值域为，求a，b的值。

     

    查看答案和解析>>

    下面几种推理是类比推理的是                          （   ）

    A．两条直线平行，同旁内角互补，如果和是两条平行直线的同旁内角，则
    B．由平面向量的运算性质，推测空间向量的运算性质
    C．某校高二级有20个班，1班有51位团员，2班有53位团员，3班有52位团员，由此可以推测各班都超过50位团员,；
    D．一切偶数都能被2整除，是偶数，所以能被2整除

    查看答案和解析>>


    同步练习册答案