已知均为正数，，则的最小值是            （    ）

         A．            B．           C．             D．

第Ⅱ卷  （非选择题  共90分）

二、填空题：本大题共4小题，每小题4分，共16分，将答案填在题中的横线上。

二、填空题：本大题共7小题，考生作答6小题，每小题5分，满分30分．

（一）必做题（9～13题）

9．如图1是一个空间几何体的三视图，则该几何体的体积为      ．

第Ⅱ卷(非选择题,共90分)

二、填空题：（本大题4小题，每小题5分，满分20分）

13．用一个平面去截正方体，其截面是一个多边形，则这个多边形的边数最多是     条 。

 [番茄花园1] 设O为坐标原点，,是双曲线（a＞0，b＞0）的焦点，若在双曲线上存在点P，满足∠P=60°，∣OP∣=,则该双曲线的渐近线方程为

（A）x±y=0          （B）x±y=0

（C）x±=0         （D）±y=0

非选择题部分（共100分）

二，填空题：本大题共7小题，每小题4分，共28分。

 [番茄花园1]1.

二、填空题：（本大题共4小题，每小题5分，共20分．把答案填在

答题卡的相应位置．）

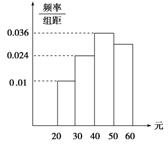
13．学校为了调查学生在课外读物方面的支出情况，抽出了一个容量    

为n的样本，其频率分布直方图如图所示，其中支出在[50,60)

元的同学有30人，则n的值为________．