练习册

  • 练习册
  • 试题
    已知抛物线. (Ⅰ)若..求该抛物线与轴公共点的坐标, (Ⅱ)若.且当时.抛物线与轴有且只有一个公共点.求的取值范围, (Ⅲ)若.且时.对应的,时.对应的.试判断当时.抛物线与轴是否有公共点?若有.请证明你的结论,若没有.阐述理由． 解(Ⅰ)当.时.抛物线为. 方程的两个根为.． ∴该抛物线与轴公共点的坐标是和． ················································ 2分 (Ⅱ)当时.抛物线为.且与轴有公共点． 对于方程.判别式≥0.有≤． ········································ 3分 ①当时.由方程.解得． 此时抛物线为与轴只有一个公共点．································· 4分 ②当时. 时.. 时.． 由已知时.该抛物线与轴有且只有一个公共点.考虑其对称轴为. 应有 即 解得． 综上.或． ················································································ 6分 (Ⅲ)对于二次函数. 由已知时.,时.. 又.∴． 于是．而.∴.即． ∴． ············································································································ 7分 ∵关于的一元二次方程的判别式 . ∴抛物线与轴有两个公共点.顶点在轴下方．····························· 8分 又该抛物线的对称轴. 由... 得. ∴． 又由已知时.,时..观察图象. 可知在范围内.该抛物线与轴有两个公共点． ············································ 10分 【查看更多】

     

    题目列表(包括答案和解析)

    已知n是正整数，pn(xn,yn)是反比例函数y=的图象上的一列点，其中x1=1，x2=2，…，xn=n,记

    T1= x1y2，T2= x2y3，…，T8= x8y9；若T1=1，则T1 •T2 • … •T8的值是__________.（08衢州卷第16题改编）

    查看答案和解析>>

    李明在一次测验中做了2道习题，请你判断他是否都正确，若有不正确，请在答题卷相应题号后写上不正确，并写出正确的解答；若正确，则只在答题卷的相应题号后写上“正确”即可
    （1）解不等式组
    1-
    x+1
    3
    ≥0(1)
    3-4(x-1)＜1(2)

    由（1）得x≤2；
    由（2）得x＞
    3
    2

    ∴
    3
    2
    ＜x≤2
    （2）计算
    		4
    +(
    1
    2
    )-1-2cos60°+(2-π)0
    =2+2-1+1=4．

    查看答案和解析>>

    李明在一次测验中做了3道习题，请你判断他是否都正确，若有不正确，请在答题卷相应题号后写上不正确，并写出正确的解答；若正确，则只在答题卷的相应题号后写上“正确”即可．
    ①化简(
    1
    1-x
    -
    1
    1+x
    )÷(
    x
    x2-1
    +x)
    =
    1+x-1+x
    1-x2
    ×
    x2-1
    x
    +
    1+x-1+x
    1-x2
    ×
    1
    x
    =-2+
    2
    1-x2
    =
    2x2
    1-x2

    ②解不等式组
    1-
    x+1
    3
    ≥0(1)
    3-4(x-1)＜1(2)
    由（1）得x≤2；  由（2）得x＞
    3
    2

    ∴
    3
    2
    ＜x≤2
    ③计算
    		4
    +(
    1
    2
    )-1-2cos60°+(2-π)0    =2+2-1+1=4．

    查看答案和解析>>

    已知抛物线M：y = -x2+2mx+n（m，n为常数，且m> 0，n>0）的顶点为A，与y轴交于点C；抛物线N与抛物线M关于y轴对称，其顶点为B，连结AC，BC，AB．

    问抛物线M上是否存在点P，使得四边形ABCP为菱形？如果存在，请求出m的值；如果不存在，请说明理由．

    说明：⑴如果你反复探索,没有解决问题, 请写出探索过程(要求至少写3步)；

    ⑵在你完成⑴之后,可以从①、②中选取一个条件，完成解答（选取①得7分；选取②得10分）．

    ①；②．

    附加题: 若将26题中“抛物线M：y= -x2+2mx+n（m，n为常数，且m> 0，n>0） ”改为“抛物线M：y= ax2+2mx+n（m，n为常数，且m≠ 0,a≠0, n>0） ”，其他条件不变, 探究 26题中问题．

    查看答案和解析>>

    李明在一次测验中做了3道习题，请你判断他是否都正确，若有不正确，请在答题卷相应题号后写上不正确，并写出正确的解答；若正确，则只在答题卷的相应题号后写上“正确”即可．
    ①化简
    =
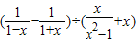
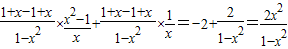
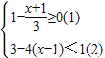    ②解不等式组由（1）得x≤2；  由（2）得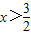
    ∴
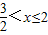
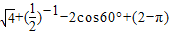    ③计算=2+2-1+1=4．

    查看答案和解析>>


    同步练习册答案