
题目列表(包括答案和解析)
导数的概念
(1)对于函数y=f(x),我们把式子![]() 称为函数f(x)从x1到x2的_________.换言之,如果自变量x在x0处有增量Δx,那么函数f(x)相应地有增量_________;比值_________就叫做函数y=f(x)在x0到x0+Δx之间的_________.
称为函数f(x)从x1到x2的_________.换言之,如果自变量x在x0处有增量Δx,那么函数f(x)相应地有增量_________;比值_________就叫做函数y=f(x)在x0到x0+Δx之间的_________.
(2)函数y=f(x)在x=x0处的瞬时变化率是_________,我们称它为函数y=f(x)在x=x0处的_________,记作_________,即![]() (x0)=_________.
(x0)=_________.
(3)函数f(x)的导数![]() (x)就是x的一个函数.我们称它为f(x)的_________,简称_________,记作_________.
(x)就是x的一个函数.我们称它为f(x)的_________,简称_________,记作_________.
导数的概念
(1)对于函数y=f(x),如果自变量x在x0处有增数Δx,那么函数y相应地有增量_________;比值_________就叫做函数y=f(x)在x0到x0+Δx之间的_________.
(2)当Δx→0时,![]() 有极限,我们就说y=f(x)在点x0处_________,并把这个极限叫做f(x)在点x0处的导数(或变化率)记作_________或_________,即
有极限,我们就说y=f(x)在点x0处_________,并把这个极限叫做f(x)在点x0处的导数(或变化率)记作_________或_________,即![]() (x0)=_________=_________,函数f(x)的导数
(x0)=_________=_________,函数f(x)的导数![]() (x)就是当Δx→0时,函数的增量Δy与自变量的增量Δx的比
(x)就是当Δx→0时,函数的增量Δy与自变量的增量Δx的比![]() 的极限,即
的极限,即![]() (x)=_________=_________.
(x)=_________=_________.
函数 在
在 处导数
处导数 的几何意义是
( )
的几何意义是
( )
A. 在点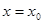 处的斜率;
处的斜率;
B. 在点 处的切线与
处的切线与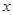 轴所夹的锐角正切值;
轴所夹的锐角正切值;
C. 点 与点
与点 连线的斜率;
连线的斜率;
D. 曲线 在点
在点 处的切线的斜率.
处的切线的斜率.
函数 在
在 处导数
处导数 的几何意义是( )
的几何意义是( )
A. 在点 处的斜率;
处的斜率;
B. 在点 ( x0,f ( x0 ) ) 处的切线与 轴所夹的锐角正切值;
轴所夹的锐角正切值;
C. 点 ( x0,f ( x0 ) ) 与点 (0 , 0 ) 连线的斜率;
D. 曲线 在点
( x0,f ( x0 ) ) 处的切线的斜率.
在点
( x0,f ( x0 ) ) 处的切线的斜率.
| 吃零食 | 不吃零食 | 合计 |
男学生 | 24 | 31 | 55 |
女学生 | 8 | 26 | 34 |
合计 | 32 | 57 | 89 |
根据上述数据分析,我们得出的χ2=___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com