
题目列表(包括答案和解析)
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
|
|
男 |
女 |
总计 |
|
爱好 |
40 |
20 |
60 |
|
不爱好 |
20 |
30 |
50 |
|
总计 |
60 |
50 |
110 |
由K2= 算得,K2=
算得,K2=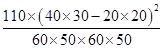 ≈7.8.
≈7.8.
附表:
|
P(K2≥k) |
0.050 |
0.010 |
0.001 |
|
k |
3.841 |
6.635 |
10.828 |
参照附表,得到的正确结论是( )
A.有99%以上的把握认为“爱好该项运动与性别有关”
B.有99%以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
下列推理是归纳推理的是( )
A.A,B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆
B.由a1=1,an=3n-1(n>1),求出S1,S2,S3,猜想数列的前n项和Sn的表达式
C.由圆x2+y2=r2的面积πr2,猜出椭圆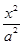 +
+ =1的面积S=πab
=1的面积S=πab
D.科学家利用鱼的沉浮原理制造潜艇
下面给出的解答中,正确的是( ).
(A)y=x+≥2=2,∴y有最小值2
(B)y=|sinx|+≥2=4,∴y有最小值4
(C)y=x(-2x+3)≤=,又由x=-2x+3得x=1,∴当x=1时,y有最大值=1
(D)y=3-- ≤3-2=-3,y有最大值-3
在△ABC中,a、b、c分别是角A、B、C的对边,cosB= .
.
⑴ 若cosA=- ,求cosC的值; ⑵
若AC=
,求cosC的值; ⑵
若AC= ,BC=5,求△ABC的面积.
,BC=5,求△ABC的面积.
【解析】第一问中sinB=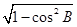 =
= , sinA=
, sinA= =
=
cosC=cos(180°-A-B)=-cos(A+B) =sinA.sinB-cosA·cosB
= ×
× -(-
-(- )×
)× =
=
第二问中,由 =
= +
+ -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10= +25-8AB
+25-8AB
解得AB=5或AB=3综合得△ABC的面积为 或
或
解:⑴ sinB=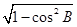 =
= , sinA=
, sinA= =
= ,………………2分
,………………2分
∴cosC=cos(180°-A-B)=-cos(A+B) ……………………3分
=sinA.sinB-cosA·cosB ……………………4分
= ×
× -(-
-(- )×
)× =
= ……………………6分
……………………6分
⑵ 由 =
= +
+ -2AB×BC×cosB得 10=
-2AB×BC×cosB得 10= +25-8AB
………………7分
+25-8AB
………………7分
解得AB=5或AB=3, ……………………9分
若AB=5,则S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×5×
×5×5× =
= ………………10分
………………10分
若AB=3,则S△ABC= AB×BC×sinB=
AB×BC×sinB= ×5×3×
×5×3× =
= ……………………11分
……………………11分
综合得△ABC的面积为 或
或
下列推理是归纳推理的是( )
A. A、B为定点,动点P满足|PA|+|PB|=2a>|AB|,得P的轨迹为椭圆
B. 由a1=1,an=3n-1,求出S1,S2,S3,猜想出数列的前n项和Sn的表达式
C. 由圆x2+y2=r2的面积πr2,猜出椭圆![]() +
+![]() =1的面积S=πab
=1的面积S=πab
D. 科学家利用鱼的沉浮原理制造潜艇
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com