（2008•佛山二模）如图，四条直线互相平行，且相邻两条平行线的距离均为h，一直正方形的4个顶点分别在四条直线上，则正方形的面积为（　　）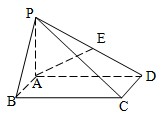

（2008•闸北区二模）如图，在底面是矩形的四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB=1，BC=2．
（Ⅰ）求PC与平面PAD所成角的大小；
（Ⅱ）若E是PD的中点，求异面直线AE与PC所成角的大小；
（Ⅲ）在BC边上是否存在一点G，使得D点到平面PAG的距离为

2

，若存在，求出BG的值；若不存在，请说明理由．

（2013•南通三模）已知函数f(x)=

ax2-2x-1，x≥0 x2+bx+c，x＜0

是偶函数，直线y=t与函数y=f（x）的图象自左向右依次交于四个不同点A，B，C，D．若AB=BC，则实数t的值为．

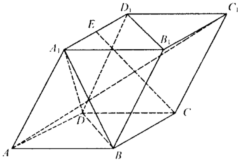（2008•成都三模）已知平行六面体ABCD-A₁B₁C₁D₁中，∠A₁AD=∠A₁AB=∠BAD=60°，AA₁=AB=AD，E为A₁D₁的中点．给出下列四个命题：①∠BCC₁为异面直线AD与CC₁所成的角；②三棱锥A₁-ABD是正三棱锥；③CE⊥平面BB₁D₁D；④

CE

=-

1

2

AD

-

AB

+

AA1

．其中正确的命题有．（写出所有正确命题的序号）

9、如图所示是2008年北京奥运会的会徽，其中的“中国印”由四个色块构成，可以用线段在不穿越其他色块的条件下将其中任意两个色块连接起来（如同架桥），如果用三条线段将这四个色块连接起来，不同的连接方法共有（　　）