练习册

  • 练习册
  • 试题
    案例中.学生能在教师的引导下.不但能在对图形进行直观观察的基础上用割补法.相似的性质.等底等高面积法等方法解决问题.而且会由25与50的关系大胆猜想:无论在什么情况下的面积刚好等于正方形ABCD的面积的一半.且与小正方形的面积无关.最难能可贵的是学生在解决此问题时能利用解决问题的特殊法过渡到一般法.并且学生F能从纷繁复杂的图形中观察出“等底等高 这一主要的特征.并用这一特征轻松地说明.解决问题.在整个过程中处处体现了学生主动探索.教师适当引导的融洽交流情景.学生的思维也得到了充分的拓展.这说明了一个问题:若我们教师能积极创设情景.不断给学生思维的契机.处处设疑.激疑.释疑.我想这样必定会激发学生学习的热情.好奇心.从而引发学生创造性思维. 而对于教师来说.本人觉得:首先张老师能打破传统习题课的框架.将解题的过程成为学生自己探索和发现的过程.而不是教师对求解模式的介绍过程.在这个过程中.引导学生深入思考.解决问题.并抓住时机引导学生探索出的面积与小正方形的面积无关这一隐含性结论,其次.他能够带领学生对一个问题进行横纵向地深入学习.探究.而不是像我们一般的习题课那样只是为了解题而解题.并且能在教学中及时渗透解决问题的一般法与特殊法.直接法与间接法.割补法.分类讨论等数学思想方法.总的来说.整个案例体现了张老师教学过程思路清晰.突出思维的主题.设问架桥.引导学生思维层层拔高.是符合“新课标 思想要求.符合新的教育理念和教学策略的.我们应该学习和借鉴他的做法. 【查看更多】

     

    题目列表(包括答案和解析)

    下列关于框图的逻辑结构正确的是（　　）

    查看答案和解析>>

    4、下列命题不是全称命题的是（　　）

    查看答案和解析>>

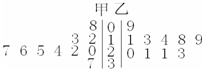    精英家教网某篮球队甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个．命中个数的茎叶图如右图所示．则下面结论中错误的一个是（　　）
    A、甲的中位数是21B、乙的众数是21C、甲罚球命中率比乙高D、甲的极差是29

    查看答案和解析>>

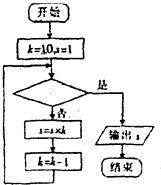    4、下面是一算法的程序框图，如果上述程序运行结果为S=90，那么判断框中应填入关于k的判断条件是（　　）
    （注：框图中的赋值符号”=”也可以写出“←”或“：=”）

    查看答案和解析>>

    一组数据20，30，40，50，50，60，70，80的平均数、中位数、众数的大小关系是（　　）

    查看答案和解析>>


    同步练习册答案