练习册

  • 练习册
  • 试题
    在解决问题的过程中.张老师绝大部分是让学生进行探究的.但有一个地方本人认为他可以更加大胆的放手让学生探究.如刚好计算出的面积等于正方形ABCD的面积的一半时.他无意中已用设问的方式道出了“的面积与小正方形面积无关 这一本质问题.从表面上看.好像是在引导学生思考.实际上是牵着学生的鼻子走.没有让学生进行真正的探索和让学生根据自己的实际建构提出问题.没有真正达到开发学生思维潜力的目的.反而把原本有探究价值且可由学生独立探究的问题分解为一小块一小块.其实.张老师可直接问学生:“你们由此发现了怎样的事实? 而不要把实质问题“的面积与小正方形面积无关 用设问的方式导出来.我想.若能长期这样训练下去必定会提高学生的“数感 和对数学的敏感度. 在本案例中.还有一个问题值得我们深思:就是在解决完一道例题后我们教师该做怎样的工作.使学生有进一步的收获?在本案例中没有反映出这一点.本人觉得:问题解决完后教师应带领学生进行深入的自我总结.把问题上升到理性认识.在解决完本例题后.若张老师能带领学生回过头再一次用审视的眼光评析他们的所做.评析他们的思考方式.评析他们的所得.那该多好呀! 为什么本人会有这种想法呢?因为本人觉得从高一点的角度看.解题的目的主要有二个:一是学科意义上的价值.即通过解题.进一步熟悉.理解所学内容.在内容间建立起联系,二是人生意义上的价值.也是根本所在.即通过解题.让学生从成功中发现自我.培养自信.坚强.忍耐的品格.所以.我们教师应该帮助学生养成自觉反思的习惯.总结解题过程中的经验.学会寻找新旧知识间的联系.寻找解决此类问题的一般解法和在解决问题的过程中如何突破自己思维框架等等.把思维的“网口 有目的地拉大.逐步培养思维的创造力. 最后.我还在想:若我们教师能真正给时间给空间学生进行探究.我们整个教育将会是怎样的一番景象呢?这还有待我们大家去探讨. 【查看更多】

     

    题目列表(包括答案和解析)

    下列关于算法的叙述不正确的是（　　）

    查看答案和解析>>

    在解决下列各问题的算法中，一定用到循环结构的是（　　）
    A、求函数f（x）=3x2-2x+1当x=5时的值
    B、用二分法求
    		3
    发近似值
    C、求一个给定实数为半径的圆的面积
    D、将给定的三个实数按从小到大排列

    查看答案和解析>>

    下列四个有关算法的说法中，正确的是（　　）
    ①算法的各个步骤是可逆的  ②算法执行后一定得到确定的结果  ③解决某类问题的算法不是唯一的  ④算法一定在有限多步内结束．

    查看答案和解析>>

    为解决四个村庄用电问题，政府投资在已建电厂与这四个村庄之间架设输电线路，现已知这四个村庄及电厂之间的距离如图所示（距离单位：公里）则能把电力输送到这四个村庄的输电线路的最短总长度应该是（　　）

    查看答案和解析>>

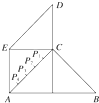    某县位于山区，居民的居住区域大致呈如右图所示的五边形，近似由一个正方形和两个等腰直角三角形组成，若AB=60km，AE=CD=30km，为了解决当地人民看电视难的问题，准备建一个电视转播台，理想方案是转播台距五边形各顶点的距离平方和最小，图中P1、P2、P3、P4是AC的五等分点，则转播台应建在（　　）

    查看答案和解析>>


    同步练习册答案