（本题满分13分）在4月份（按30天计算），有一新款服装投入某商场销售，4月1日该款服装仅销售出10件，第二天售出35件，第三天销售60件，然后，每天售出的件数分别递增25件，直到4月12日销售量达到最大，以后每天销售的件数分别递减15件.

（Ⅰ）问到月底该服装共销售出几件．

（Ⅱ）按规律，当该商场销售此服装的日销售量达到150件以上时，社会上就流行，问该款服装在社会上流行是否超过14天？并说明理由.

(本题满分13分)本题共有2个小题，第一个小题满分5分，第2个小题满分8分。

已知数列的前项和为，且，

（1）证明：是等比数列；

（2）求数列的通项公式，并求出n为何值时，取得最小值，并说明理由。

   （2）=  n=15取得最小值

（本题满分13分）我炮兵阵地位于地面A处，两观察所分别位于地面点C和D处，已知CD=6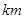，∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时，测得∠BCD=30°，∠BDC=15°(如图），求炮兵阵地到目标的距离.

(本题满分13分)本题共有2个小题，第一个小题满分5分，第2个小题满分8分。

已知数列的前项和为，且，

（1）证明：是等比数列；

（2）求数列的通项公式，并求出n为何值时，取得最小值，并说明理由。

   （2）=  n=15取得最小值

（本题满分13分）在4月份（按30天计算），有一新款服装投入某商场销售，4月1日该款服装仅销售出10件，第二天售出35件，第三天销售60件，然后，每天售出的件数分别递增25件，直到4月12日销售量达到最大，以后每天销售的件数分别递减15件.

（Ⅰ）问到月底该服装共销售出几件．

（Ⅱ）按规律，当该商场销售此服装的日销售量达到150件以上时，社会上就流行，问该款服装在社会上流行是否超过14天？并说明理由.