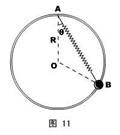
如图11所示，一个重量为G的小球套在竖直放置的、半径为R的光滑大环上，另一轻质弹簧的劲度系数为k ，自由长度为L(L＜2R)，一端固定在大圆环的顶点A ，另一端与小球相连。环静止平衡时位于大环上的B点。试求弹簧与竖直方向的夹角θ。

如图5－11所示，一轻绳绕过无摩擦的两个轻质小定滑轮O₁、O₂和质量m_B=m的小球连接，另一端与套在光滑直杆上质量m_A=m的小物块连接，已知直杆两端固定，与两定滑轮在同一竖直平面内，与水平面的夹角θ=60°，直杆上C点与两定滑轮均在同一高度，C点到定滑轮O₁的距离为L，重力加速度为g，设直杆足够长，小球运动过程中不会与其他物体相碰．现将小物块从C点由静止释放，试求：

小球下降到最低点时，小物块的机械能（取C点所在的水平面为参考平面）；

小物块能下滑的最大距离；

小物块在下滑距离为L时的速度大小．

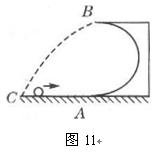
如图11所示，一半径为R的光滑半圆形轨道AB固定在水平地面上，一个质量为m的小球以某一速度从半圆形轨道的最低点A冲上轨道，当小球将要从轨道最高点B飞出时，小球对轨道的压力为3mg（g为重力加速度），求：

（1）小球在半圆形轨道最高点时的加速度大小；

（2）小球的落地点C离A点的水平距离。

（8分）如图11所示，一半径为R的光滑半圆形轨道AB固定在水平地面上，一个质量为m的小球以某一速度从半圆形轨道的最低点A冲上轨道，当小球将要从轨道最高点B飞出时，小球对轨道的压力为3mg（g为重力加速度），求：

（1）小球在半圆形轨道最高点时的加速度大小；

（2）小球的落地点C离A点的水平距离。