
题目列表(包括答案和解析)
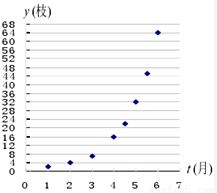
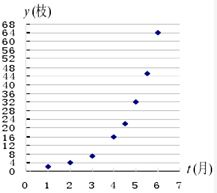 18、如图给出了某种豆类生长枝数y(枝)与时间t(月)的散点图,那么此种豆类生长枝数与时间的关系用下列函数模型近似刻画最好的是( )
18、如图给出了某种豆类生长枝数y(枝)与时间t(月)的散点图,那么此种豆类生长枝数与时间的关系用下列函数模型近似刻画最好的是( )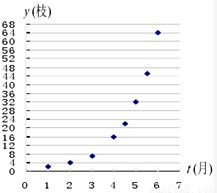
年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/cm | 90.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
(1)年龄(解释变量)和身高(预报变量)之间具有怎样的相关关系?
(2)如果年龄相差5岁,则身高有多大差异?(3~16岁之间)
(3)如果身高相差20 cm,其年龄相差多少?
(4)计算残差,说明该函数模型能够较好地反映年龄与身高的关系吗?请说明理由?
年龄/周岁 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
身高/cm | 90.8 | 97.6 | 104.2 | 110.9 | 115.6 | 122.0 | 128.5 |
年龄/周岁 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
身高/cm | 134.2 | 140.8 | 147.6 | 154.2 | 160.9 | 167.5 | 173.0 |
(1)年龄(解释变量)和身高(预报变量)之间具有怎样的相关关系?
(2)如果年龄相差5岁,则身高有多大差异?(3~16岁之间)
(3)如果身高相差20 cm,其年龄相差多少?
(4)计算残差,说明该函数模型能够较好地反映年龄与身高的关系吗?请说明理由?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com