（本小题满分12分）
设函数.
（Ⅰ）若当时取得极值，求a的值，并讨论的单调性；
（Ⅱ）若存在极值，求a的取值范围，并证明所有极值之和大于.
请考生在第22、23、24题中任选一题做答，如果多做，则按所做的第一题记分。做答时请写清题号。

（本小题满分12分）

设函数.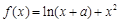

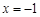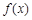（Ⅰ）若当时取得极值，求a的值，并讨论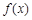的单调性；

（Ⅱ）若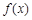存在极值，求a的取值范围，并证明所有极值之和大于.

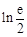请考生在第22、23、24题中任选一题做答，如果多做，则按所做的第一题记分。做答时请写清题号。

设是定义在R上的奇函数，与的图象关于直线x = 1对称，当时，。

（1）求的解析式；

（2）当x = 1时，取得极值，证明：对任意x₁、，不等式

。

（3）若是上的单调函数，且当时有，

证明：。

已知函数的图象过坐标原点O,且在点处的切线的斜率是.

（Ⅰ）求实数的值； 

（Ⅱ）求在区间上的最大值；

（Ⅲ）对任意给定的正实数，曲线上是否存在两点P、Q，使得是以O为直角顶点的直角三角形，且此三角形斜边中点在轴上？说明理由.

【解析】第一问当时，，则。

依题意得：，即    解得

第二问当时，，令得，结合导数和函数之间的关系得到单调性的判定，得到极值和最值

第三问假设曲线上存在两点P、Q满足题设要求，则点P、Q只能在轴两侧。

不妨设，则，显然

∵是以O为直角顶点的直角三角形，∴

即    （*）若方程（*）有解，存在满足题设要求的两点P、Q；

若方程（*）无解，不存在满足题设要求的两点P、Q.

（Ⅰ）当时，，则。

依题意得：，即    解得

（Ⅱ）由（Ⅰ）知，

①当时，，令得

当变化时，的变化情况如下表：

又，，。∴在上的最大值为2.

②当时, .当时, ,最大值为0；

当时, 在上单调递增。∴在最大值为。

综上，当时，即时，在区间上的最大值为2；

当时，即时，在区间上的最大值为。

（Ⅲ）假设曲线上存在两点P、Q满足题设要求，则点P、Q只能在轴两侧。

不妨设，则，显然

∵是以O为直角顶点的直角三角形，∴

即    （*）若方程（*）有解，存在满足题设要求的两点P、Q；

若方程（*）无解，不存在满足题设要求的两点P、Q.

若，则代入（*）式得：

即，而此方程无解，因此。此时，

代入（*）式得：    即   （**）

令 ，则

∴在上单调递增，  ∵     ∴,∴的取值范围是。

∴对于，方程（**）总有解，即方程（*）总有解。

因此，对任意给定的正实数，曲线上存在两点P、Q，使得是以O为直角顶点的直角三角形，且此三角形斜边中点在轴上