根据上表的内容并结合图象.试总结函数, , ,, 的共同性质. 【查看更多】

同学们会面对一个共同的问题，就是有时有太多的事情要做．例如，你可能面临好几门课的作业的最后期限，你如何合理安排以确保每门课的作业都能如期完成？如果根本不可能全部按期完成，你怎么办？

　　这里给出的霍奇森(Hodgson)算法，可以使得迟交作业的数目减到最小．这一算法已经广泛应用于工业生产安排的实践中．

假设你知道各项作业的到期日，并且知道或能估计出完成每项作业将花费的时间，下面是这个算法的自然语言表述：

　　第一步　把这些作业按到期日的顺序从左到右排列，从最早到期的到最晚到期的；

　　第二步　假设从左到右一项一项做这些作业的话，计算出从开始到完成某一项作业时所花的时间．依次做此计算直到完成了所列表中的全部作业而没有一项作业会超期，停止；或你算出某项作业将会超期，继续第三步；

　　第三步　考虑第一项将会超期的作业以及它左边的所有作业，从中取出花费时间最长的那项作业，并把它从表中去掉；

　　第四步　回到第二步，并重复第二到四步，直到做完．

　　根据上表，按霍奇森算法，写出程序框图和程序．

为了了解某班学生每周做家务劳动的时间，某综合实践活动小组对该班50名学生进行了调查，有关数据如下表：

每周做家务的时间（小时）	0	1	1.5	2	2.5	3	3.5	4
人数（人）	2	2	6	8	12	13	4	3

　　根据上表中的数据，回答下列问题：

　　（1）该班学生每周做家务劳动的平均时间是多少小时？

　　（2）这组数据的中位数、众数分别是多少?

　　（3）请你根据（1）、（2）的结果，用一句话谈谈自己的感受．

某产品的广告费用x与销售额y的统计数据如下表
广告费用x（万元） 4 2 3 5
销售额y（万元） 49 26 39 54
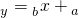　根据上表可得回归方程 $数学公式$ 中的 $数学公式$ 为9.4，据此模型预报广告费用为6万元时销售额为

假设关于某设备的使用年限x和所支出的维修费用y（万元）有如下表格所示统计数据，由资料显示y对x呈线性相关关系。

x	3	4	5	6
y	2.5	3	4	4.5

(Ⅰ)请根据上表的数据画出散点图并用最小二乘法求出y关于x的线性回归方程？

(Ⅱ)试根据(1)求出的线性回归方程，预测使用年限为10年时，维修费用是多少？

某食品厂为了检查甲乙两条自动包装流水线的生产情况，随即在这两条流水线上各抽取40件产品作为样本称出它们的重量（单位：克），重量值落在（495，510]的产品为合格品，否则为不合格品．表1是甲流水线样本频数分布表，图1是乙流水线样本的频率分布直方图．

（1）根据上表数据在答题卡上作出甲流水线样本的频率分布直方图；
（2）若以频率作为概率，试估计从乙流水线上任取5件产品，恰有3件产品为合格品的概率；
（3）由以上统计数据完成下面2×2列联表，并回答有多大的把握认为“产品的包装质量与
两条自动包装流水线的选择有关”．

P（k²≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

附：下面的临界值表供参考：
（参考公式：K2=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

，其中n=a+b+c+d）

某产品的广告费用x与销售额y的统计数据如下表广告费用x（万元）4235销售额y（万元）49263954 根据上表可得回归方程中的为9.4，据此模型预报广告费用为6万元时销售额为