
题目列表(包括答案和解析)
| 1 |
| m |
| 1 |
| n |
| 2 |
| p |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| m |
| 1 |
| n |
| 2a |
| b2 |
| 2a |
| b2 |
(此题平行班做)(本小题满分12分)
某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:


(Ⅰ)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是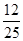 ,请完成上面的
,请完成上面的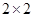 列联表;
列联表;
|
|
|
|
|
|
|
|
|
|
(Ⅱ)在(1)的条件下,试运用独立性检验的思想方法分析:在犯错误概率不超过0.1%的情况下判断学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
| 1 |
| m |
| 1 |
| n |
| 2 |
| p |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| m |
| 1 |
| n |
(本小题满分14分)
阅读下面一段文字:已知数列![]() 的首项
的首项![]() ,如果当
,如果当![]() 时,
时,![]() ,则易知通项
,则易知通项![]() ,前
,前![]() 项的和
项的和![]() . 将此命题中的“等号”改为“大于号”,我们得到:数列
. 将此命题中的“等号”改为“大于号”,我们得到:数列![]() 的首项
的首项![]() ,如果当
,如果当![]() 时,
时,![]() ,那么
,那么![]() ,且
,且![]() . 这种从“等”到“不等”的类比很有趣。由此还可以思考:要证
. 这种从“等”到“不等”的类比很有趣。由此还可以思考:要证![]() ,可以先证
,可以先证![]() ,而要证
,而要证![]() ,只需证
,只需证![]() (
(![]() ). 结合以上思想方法,完成下题:
). 结合以上思想方法,完成下题:
已知函数![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,若数列
,若数列![]() 的前
的前![]() 项的和为
项的和为![]() ,求证:
,求证:![]() .
.
| 1 |
| m |
| 1 |
| n |
| 2 |
| p |
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| m |
| 1 |
| n |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com