
题目列表(包括答案和解析)
已知直线y=kx+5与圆(x-1)2+y2=1,下列结论中正确结论的序号是________.
①直线与圆的位置关系是相离;
②直线与圆的位置关系因k值的变化而变化;
③当且仅当k=-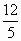 时,直线与圆相切;
时,直线与圆相切;
④若k>0时,直线与圆必然相离;
⑤圆与直线有交点的充要条件是k<-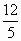 .
.
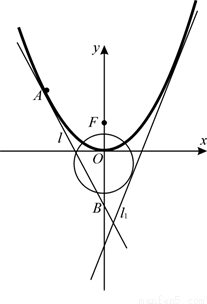
如图,已知直线 (
(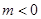 )与抛物线
)与抛物线 :
: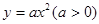 和圆
和圆 :
: 都相切,
都相切, 是
是 的焦点.
的焦点.
(Ⅰ)求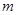 与
与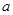 的值;
的值;
(Ⅱ)设 是
是 上的一动点,以
上的一动点,以 为切点作抛物线
为切点作抛物线 的切线
的切线 ,直线
,直线 交
交 轴于点
轴于点 ,以
,以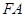 、
、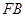 为邻边作平行四边形
为邻边作平行四边形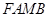 ,证明:点
,证明:点 在一条定直线上;
在一条定直线上;
(Ⅲ)在(Ⅱ)的条件下,记点 所在的定直线为
所在的定直线为 , 直线
, 直线 与
与 轴交点为
轴交点为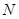 ,连接
,连接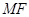 交抛物线
交抛物线 于
于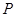 、
、 两点,求△
两点,求△ 的面积
的面积 的取值范围.
的取值范围.
【解析】第一问中利用圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去)
舍去)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
,
第二问中,由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形
, ∵四边形FAMB是以FA、FB为邻边作平行四边形
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线
第三问中,设直线 ,代入
,代入 得
得 结合韦达定理得到。
结合韦达定理得到。
解:(Ⅰ)由已知,圆 :
:
 的圆心为
的圆心为 ,半径
,半径 .由题设圆心到直线
.由题设圆心到直线 的距离
的距离 .
.
即 ,解得
,解得 (
( 舍去). …………………(2分)
舍去). …………………(2分)
设 与抛物线的相切点为
与抛物线的相切点为 ,又
,又 ,得
,得 ,
, .
.
代入直线方程得: ,∴
,∴ 所以
所以 ,
, .
……(2分)
.
……(2分)
(Ⅱ)由(Ⅰ)知抛物线 方程为
方程为 ,焦点
,焦点 . ………………(2分)
. ………………(2分)
设 ,由(Ⅰ)知以
,由(Ⅰ)知以 为切点的切线
为切点的切线 的方程为
的方程为 .
.
令 ,得切线
,得切线 交
交 轴的
轴的 点坐标为
点坐标为 所以
所以 ,
, , ∵四边形FAMB是以FA、FB为邻边作平行四边形,
, ∵四边形FAMB是以FA、FB为邻边作平行四边形,
∴ 因为
因为 是定点,所以点
是定点,所以点 在定直线
在定直线 上.…(2分)
上.…(2分)
(Ⅲ)设直线 ,代入
,代入 得
得 , ……)得
, ……)得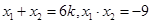 ,
…………………………… (2分)
,
…………………………… (2分)
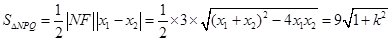 ,
,
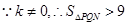 .
. △
△ 的面积
的面积 范围是
范围是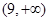
已知抛物线C: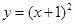 与圆
与圆 有一个公共点A,且在A处两曲线的切线与同一直线l
有一个公共点A,且在A处两曲线的切线与同一直线l
(I) 求r;
(II) 设m、n是异于l且与C及M都相切的两条直线,m、n的交点为D,求D到l的距离。
【解析】本试题考查了抛物线与圆的方程,以及两个曲线的公共点处的切线的运用,并在此基础上求解点到直线的距离。
【点评】该试题出题的角度不同于平常,因为涉及的是两个二次曲线的交点问题,并且要研究两曲线在公共点出的切线,把解析几何和导数的工具性结合起来,是该试题的创新处。另外对于在第二问中更是难度加大了,出现了另外的两条公共的切线,这样的问题对于我们以后的学习也是一个需要练习的方向。

某高中地处县城,学校规定家到学校的路程在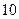 里
里
以内的学生可以走读,因交通便利,所以走读生人数很多,
该校学生会先后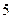 次对走读生的午休情况作了统计,得到
次对走读生的午休情况作了统计,得到
如下资料:
①若把家到学校的距离分为五个区间: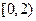 、
、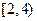 、
、 、
、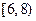 、
、 ,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
②走读生是否午休与下午开始上课的时间有着密切的关系. 下表是根据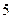 次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
| 下午开始上课时间 | 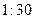 |  | 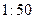 | 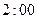 | 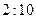 |
| 平均每天午休人数 |  |  | 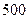 | 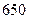 |  |
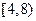 的概率是多少?
的概率是多少?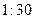 作为横坐标
作为横坐标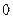 ,然后上课时间每推迟
,然后上课时间每推迟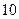 分钟,横坐标
分钟,横坐标 增加2,并以平均每天午休人数作为纵坐标
增加2,并以平均每天午休人数作为纵坐标 ,试列出
,试列出 与
与 的统计表,并根据表中的数据求平均每天午休人数
的统计表,并根据表中的数据求平均每天午休人数 与上课时间
与上课时间 之间的线性回归方程
之间的线性回归方程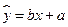 ;
; 时,家距学校的路程在4里路以下的走读生中约有多少人午休?
时,家距学校的路程在4里路以下的走读生中约有多少人午休?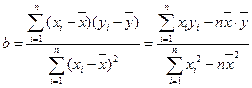 )
)某高中地处县城,学校规定家到学校的路程在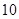 里
里
以内的学生可以走读,因交通便利,所以走读生人数很多,
该校学生会先后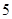 次对走读生的午休情况作了统计,得到
次对走读生的午休情况作了统计,得到
如下资料:
①若把家到学校的距离分为五个区间: 、
、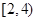 、
、 、
、 、
、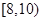 ,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
②走读生是否午休与下午开始上课的时间有着密切的关系. 下表是根据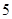 次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
|
下午开始上课时间 |
|
|
|
|
|
|
平均每天午休人数 |
|
|
|
|
|
(Ⅰ)若随机地调查一位午休的走读生,其家到学校的路程(单位:里)在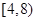 的概率是多少?
的概率是多少?
(Ⅱ)如果把下午开始上课时间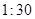 作为横坐标
作为横坐标 ,然后上课时间每推迟
,然后上课时间每推迟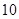 分钟,横坐标
分钟,横坐标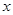 增加2,并以平均每天午休人数作为纵坐标
增加2,并以平均每天午休人数作为纵坐标 ,试列出
,试列出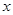 与
与 的统计表,并根据表中的数据求平均每天午休人数
的统计表,并根据表中的数据求平均每天午休人数 与上课时间
与上课时间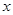 之间的线性回归方程
之间的线性回归方程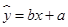 ;
;
(Ⅲ)预测当下午上课时间推迟到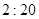 时,家距学校的路程在4里路以下的走读生中约有多少人午休?
时,家距学校的路程在4里路以下的走读生中约有多少人午休?
(注:线性回归直线方程系数公式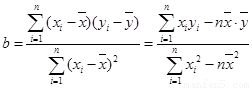 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com