
题目列表(包括答案和解析)
已知函数
(1)若 的极值点,求实数a的值;
的极值点,求实数a的值;
(2)若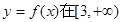 上为增函数,求实数a的取值范围;
上为增函数,求实数a的取值范围;
(3)当 有实根,求实数b的最大值。
有实根,求实数b的最大值。
【解析】本试题主要是考查了导数在研究函数中的运用。主要是极值的概念和根据单调区间,求解参数的取值范围,以及利用函数与方程的思想求解参数b的最值。
|
| x |
| 2 |
| 3 |
某单位最近组织了一次健身活动,活动分为登山组和游泳组,且每个职工至多参加了其中一组。在参加活动的职工中,青年人占42.5%,中年人占47.5%,老年人占10%。登山组的职工占参加活动总人数的![]() ,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定
,且该组中,青年人占50%,中年人占40%,老年人占10%。为了了解各组不同的年龄层次的职工对本次活动的满意程度,现用分层抽样的方法从参加活动的全体职工中抽取一个容量为200的样本。试确定
(Ⅰ)游泳组中,青年人、中年人、老年人分别所占的比例;
(Ⅱ)游泳组中,青年人、中年人、老年人分别应抽取的人数。
本小题主要考查分层抽样的概念和运算,以及运用统计知识解决实际问题的能力。
若![]() 为常数,且
为常数,且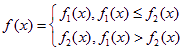 。
。
(Ⅰ)求![]() 对所有的实数
对所有的实数![]() 成立的充要条件(用
成立的充要条件(用![]() 表示);
表示);
(Ⅱ)设![]() 为两实数,
为两实数,![]() 且
且![]() ,若
,若![]() ,求证:
,求证:![]() 在区间
在区间![]() 上的单调增区间的长度和为
上的单调增区间的长度和为![]() (闭区间
(闭区间![]() 的长度定义为
的长度定义为![]() )。
)。
(本小题满分14分)若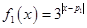 ,
,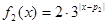 ,
,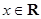 ,
,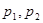 为常
为常
数,且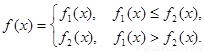
(Ⅰ)求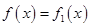 对所有实数成立的充要条件(用
对所有实数成立的充要条件(用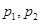 表示);
表示);
(Ⅱ)设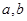 为两实数,
为两实数,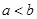 且
且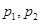
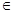
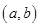 ,若
,若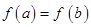
求证: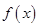 在区间
在区间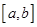 上的单调增区间的长度和为
上的单调增区间的长度和为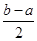 (闭区间
(闭区间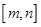 的长度定义为
的长度定义为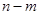 ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com