（本小题满分12分）

设双曲线的方程为，、为其左、右两个顶点，是双曲线 上的任意一点，作，，垂足分别为、，与交于点.

（1）求点的轨迹方程；

（2）设、的离心率分别为、，当时，求的取值范围.

已知定点，，动点到定点距离与到定点的距离的比值是.

（Ⅰ）求动点的轨迹方程，并说明方程表示的曲线；

（Ⅱ）当时，记动点的轨迹为曲线.

①若是圆上任意一点，过作曲线的切线，切点是，求的取值范围；

②已知，是曲线上不同的两点，对于定点，有.试问无论，两点的位置怎样，直线能恒和一个定圆相切吗？若能，求出这个定圆的方程；若不能，请说明理由.

(本题满分14分)．有一块边长为4的正方形钢板，现对其切割、焊接成一个长方体形无盖容器(切、焊损耗忽略不计)．有人应用数学知识作如下设计：在钢板的四个角处各切去一个边长为的小正方形，剰余部分围成一个长方体，该长方体的高是小正方形的边长．

(1)请你求出这种切割、焊接而成的长方体容器的的容积V₁（用表示）；

(2)经过设计（1）的方法，计算得到当时，V_l取最大值，为了材料浪费最少，工人师傅还实践出了其它焊接方法，请写出与（1）的焊接方法更佳（使材料浪费最少，容积比V_l大）的设计方案，并计算利用你的设计方案所得到的容器的容积。

（（本小题满分13分）

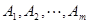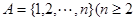若为集合且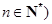的子集，且满足两个条件：

①；

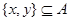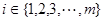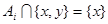②对任意的，至少存在一个，使或.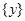

则称集合组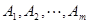具有性质.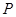

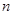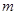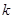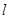如图，作行列数表，定义数表中的第行第列的数为.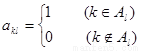

（Ⅰ）当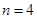时，判断下列两个集合组是否具有性质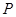，如果是请画出所对应的表格，如果不是请说明理由；

集合组1：；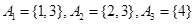

集合组2：.

（Ⅱ）当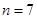时，若集合组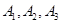具有性质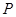，请先画出所对应的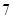行3列的一个数表，再依此表格分别写出集合；

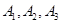（Ⅲ）当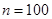时，集合组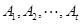是具有性质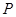且所含集合个数最小的集合组，求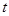的值及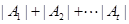的最小值.（其中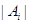表示集合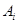所含元素的个数）

（本小题满分13分）

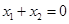  已知点是函数的图像上的两点，若对于任意实数，当时，以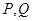为切点分别作函数的图像的切线，则两切线必平行，并且当时函数取得极小值1.[来源:]

（1）求函数的解析式；

（2）若是函数的图像上的一点，过作函数图像的切线，切线与轴和直线分别交于两点，直线与轴交于点，求△ABC的面积的最大值.