练习册

  • 练习册
  • 试题
    (1)下列函数中.表示一次函数的是 ( ) A. B. C. D. (2)已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( ) 2.[尝试] 例1.已知一次函数的图象经过点..画出函数图象,(3)函数的图象经过那些象限?(4)当增大时.的值如何? 解略(答案:.图略.图象经过一.二.四象限.随增大而减小) 例2.已知一次函数 (1)当m.n取何值时.y随x的增大而增大? (2)当m.n取何值时.直线与y轴的交点在y轴的下半轴? (3)当m.n取何值时.直线经过一.二.四象限? 分析:(1)一次函数的性质:当时.随x的增大而增大,(2)直线与y轴的交点坐标为,(3)当且一次函数的图象经过一.二.四象限. 解略.为一切实数,(2),(3)) 提炼:利用逆向思维的方法.根据一次函数的性质.体会逆向思维和定向思维的异同. 例3.已知:函数y=(m+1)x+2m﹣6 .求此函数的解析式. (2)若函数图象与直线y=2x+5平行.求其函数的解析式. 条件的直线与此同时y=﹣3x+1的交点并求这两条直线与y轴所围成的三角形面积. 分析:(1)利用函数的表达式与点的坐标的关系,(2)一次函数图象平行.表达式之间的关系,(3)利用点的坐标求线段的长.确定三角形的底和高求三角形的面积. 解:+2m﹣6 解得 m=9 ∴ y=10x+12 (2) 由题意.m+1=2 解得 m=1 ∴ y =2x﹣4 (3) 由题意得 解得: x=1,y=﹣2 ∴ 这两直线的交点是 y=2x﹣4与y轴交于 y=﹣3x+1与y轴交于(0,1) ∴S△= 提炼:利用数形结合的思想方法.根据函数的性质结合图形确定函数的解析式及三角形的面积. 例4.如图.l甲.l乙两条直线分别表示甲走路与乙骑车行走的路程S与时间t的关系.根据此图.回答下列问题: 1)乙出发时.与甲相距10km, 2)行走一段时间后.乙的自行车发生故障停下来修理.修车时间为1h, 3)乙从出发起.经过2.5h与甲相遇, 4)甲的速度为5km/h,乙的速度为15km/h, 5)甲行走的路程s之间的函数关系式是s=5t+10(t≥0), 6)在0h<t<2.5h甲走在乙的前面.在t>2.5h甲走在乙的后面, 7)如果乙的自行车不出故障.则乙出发后经过1h与甲相遇,相遇后离乙的出发点15km,在0h<t<1h范围内甲走在乙的前面.在t>1h范围内甲走在乙的后面,并在图中标出其相遇点.(相遇点为A) 提炼:运用函数的图象及性质解决实际问题.并对某些实际问题进行比较.预测.体会生活中的数学. 【查看更多】

     

    题目列表(包括答案和解析)

    观察下列数表：
    第一列 第二列 第三列 第四列
    第一行 1 2 3 4
    第二行 2 3 4 5
    第三行 3 4 5 6
    第四行 4 5 6 7
    … … … … …
    … … … … …
    （1）根据数表所反映出的规律，写出第n行第n列交叉点上的数（用含n的代数式表示）
    （2）已知k是上表中第6行第7列交叉点的数，求二次函数y=-2x2+k的图象与x轴、y轴交点的坐标．
    （3）若将y=-2x2+k的图象向下平移13个单位，写出此时的函数表达式．

    查看答案和解析>>

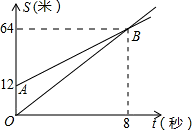    如图OB、AB分别表示甲、乙两名同学运动的一次函数图象，图中s和t分别表示运动路程和时间，已知甲的速度比乙快，下列说法：①甲让乙先跑12米；②甲的速度比乙快1.5米/秒；③8秒钟内，乙在甲前面；④8秒钟后，甲超过了乙，其中正确的说法是


    1. A.
      ①②
    2. B.
      ①②③④
    3. C.
      ②③
    4. D.
      ①③④

    查看答案和解析>>

    如图，OB、AB分别表示两名同学沿着同一路线运动的一次函数图象，图中s和t分别表示运动路程和时间，已知甲的速度比乙快．有下列结论：
    ①射线AB表示甲的运动路程与时间的函数关系；
    ②甲出发时，乙已经在甲前面12米；
    ③8秒后，甲超过了乙；
    ④64秒时，甲追上了乙．
    其中，正确结论的个数是（ ）

    A．1
    B．2
    C．3
    D．4

    查看答案和解析>>

    如图，OB、AB分别表示两名同学沿着同一路线运动的一次函数图象，图中s和t分别表示运动路程和时间，已知甲的速度比乙快．有下列结论：
    ①射线AB表示甲的运动路程与时间的函数关系；
    ②甲出发时，乙已经在甲前面12米；
    ③8秒后，甲超过了乙；
    ④64秒时，甲追上了乙．
    其中，正确结论的个数是


    1. A.
      1
    2. B.
      2
    3. C.
      3
    4. D.
      4

    查看答案和解析>>

    （2013•合肥模拟）观察下列数表：
    第一列 第二列 第三列 第四列
    第一行 1 2 3 4
    第二行 2 3 4 5
    第三行 3 4 5 6
    第四行 4 5 6 7
    … … … … …
    … … … … …
    （1）根据数表所反映出的规律，写出第n行第n列交叉点上的数（用含n的代数式表示）
    （2）已知k是上表中第6行第7列交叉点的数，求二次函数y=-2x2+k的图象与x轴、y轴交点的坐标．
    （3）若将y=-2x2+k的图象向下平移13个单位，写出此时的函数表达式．

    查看答案和解析>>


    同步练习册答案