
题目列表(包括答案和解析)
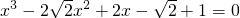 ,这是一个高次方程,我们未学过其解法,难以求解.如果我们换一个角度(“已知”和“未知”互换),即将
,这是一个高次方程,我们未学过其解法,难以求解.如果我们换一个角度(“已知”和“未知”互换),即将 看做“未知数”,而将x看成“已知数”,则原方程可整理成:
看做“未知数”,而将x看成“已知数”,则原方程可整理成: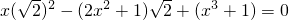 .
.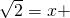 1或
1或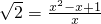 .
.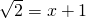 和一个一元二次方程x2-x+1=
和一个一元二次方程x2-x+1= ,从而不难求得这个高次方程的解.
,从而不难求得这个高次方程的解.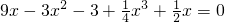 .
.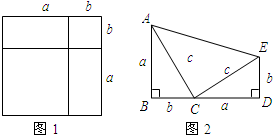 (1)如图1是一个重要公式的几何解释,请你写出这个公式______;在推得这个公式的过程中,主要运用了______
(1)如图1是一个重要公式的几何解释,请你写出这个公式______;在推得这个公式的过程中,主要运用了______| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2011 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2011 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2011 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
| 1 |
| 2011 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2010 |
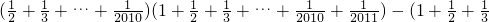
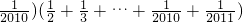
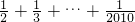 =x,先运用整体思想将原式代换,再进行整式的运算,就简单了”.小明采用小亮的思路,很快就计算出了结果,请你根据小亮的思路完成计算.
=x,先运用整体思想将原式代换,再进行整式的运算,就简单了”.小明采用小亮的思路,很快就计算出了结果,请你根据小亮的思路完成计算.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com