
题目列表(包括答案和解析)
时钟上的时针、分针像两个运动员,绕着它们的跑道昼夜不停,一直向前,分针每小时转360度,即每分钟转了6度,时针速度是分针的![]() ,即每分钟转了
,即每分钟转了![]() 度,你能进一步探索它们的运动规律,提出一些需应用一元一次方程解决的问题吗?
度,你能进一步探索它们的运动规律,提出一些需应用一元一次方程解决的问题吗?
问题1:在3点与4点之间,时钟的时针与分针什么时候重合?
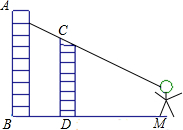 身高1.7米的小明站在平坦的公路上,见前方有AB,CD两建筑物,这时还能从CD的上端见到AB的一部分,且他的视线与水平线的夹角α=30°,已知CD=16.7米高,若小明继续向前走到N的位置时,AB刚好被CD遮住,此时他的视线与水平线的夹角β=45°,则小明从M向N行进了
身高1.7米的小明站在平坦的公路上,见前方有AB,CD两建筑物,这时还能从CD的上端见到AB的一部分,且他的视线与水平线的夹角α=30°,已知CD=16.7米高,若小明继续向前走到N的位置时,AB刚好被CD遮住,此时他的视线与水平线的夹角β=45°,则小明从M向N行进了| 3 |
| 3 |
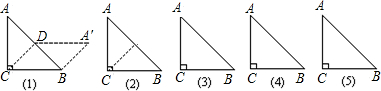
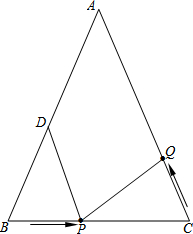 如图,在△ABC中,AB=AC=20cm,BC=16cm,点D是AB边的中点.点P是BC边上的动点,以3cm/秒的速度从点B向点C运动;点Q是AC边上的动点,同时从点C向点A运动.设运动时间为t cm/秒.
如图,在△ABC中,AB=AC=20cm,BC=16cm,点D是AB边的中点.点P是BC边上的动点,以3cm/秒的速度从点B向点C运动;点Q是AC边上的动点,同时从点C向点A运动.设运动时间为t cm/秒.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com