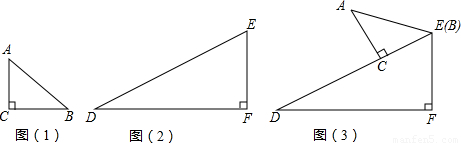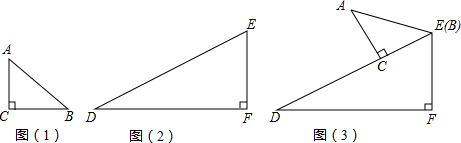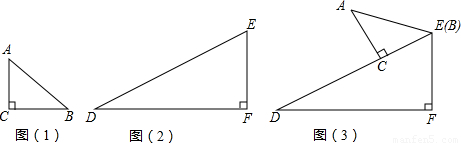如图①、②是小明在一次课外活动中剪的两块直角三角形硬纸板．图①中，∠C=90°，∠A=45°，AC=4cm；图②中，∠F=90°，∠D=30°，EF=6cm．操作：小明将两块三角形硬纸板如图③所示放置，将△ABC的直角边CB与△DEF的斜边DE重合，点B与点E重合，使△ABC沿ED方向向下滑动，当点C与点D重合时停止运动．
解决问题：
（1）在△ABC沿ED方向滑动的过程中，A、E两点间的距离逐渐______．（填“不变”、“变大”或“变小”）．
（2）假如△ABC沿ED方向以每秒1cm的速度向下滑，小明经过进一步地探究，设想了如下几个问题：
问题①：当△ABC向下滑动多少秒，A、E的连线与DF平行？
问题②：在△ABC向下滑动多少秒，以线段DC、AE、EF的长度为三边长的三角形恰好构成直角三角形？
问题③：在△ABC向下滑动的过程中，是否存在某个位置，使得∠AEC=15°？如果存在，求出下滑时间；如果不存在，请说明理由．请你分别完成上述三个问题的解答过程．