
题目列表(包括答案和解析)
18(本小题满分12分)
下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x(吨)与相应的
生产能耗y(吨标准煤)的几组对照数据。
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=![]()
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
(18) (本小题满分12分)(注意:在试用题卷上作答无效)在![]() 中,内角A、b、c的对边长分别为a、b、c.已知
中,内角A、b、c的对边长分别为a、b、c.已知![]() ,且
,且![]() ,求b.
,求b.
18(本小题满分12分)
下表提供了某厂节能降耗技术改进后生产甲产品过程中记录的产量x(吨)与相应的
生产能耗y(吨标准煤)的几组对照数据。
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程y=![]()
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤,试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
(07年安徽卷)(本小题满分14分)
如图,在六面体![]() 中,四边形ABCD是边
中,四边形ABCD是边
长为2的正方形,四边形![]() 是边长为1的正方
是边长为1的正方
形,![]() 平面
平面![]() ,
,![]() 平面ABCD,
平面ABCD,
![]()
求证: (Ⅰ)![]() 与
与![]() 共面,
共面,![]() 与
与![]() 共面.
共面.
(Ⅱ)求证:平面![]()
(Ⅲ)求二面角![]() 的大小(用反三角函数值表示).
的大小(用反三角函数值表示).
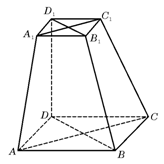
第(17)题图
(08年安徽信息交流文)(本小题满分12分)某种项目的射击比赛规定:开始时在距离目标100m处射击,如果命中记3分,同时停止射击;若第一次射击未命中目标,可以进行第二次射击,但目标已在150m远处,这时命中记2分,同时停止射击;若第二次射击仍未命中,可以进行第三次射击,但目标已在200m远处,这时命中记1分,同时停止射击。已知M射手在100m处命中目标的概率为![]() ,若他命中目标的概率与距离的平方成反比,且各次射击都是独立的。
,若他命中目标的概率与距离的平方成反比,且各次射击都是独立的。
(1)求M射手在150m处命中目标的概率;
(2)求M射手得1分的概率;
(3)求M射手在三次射击中命中目标的概率.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com