题目列表(包括答案和解析)
（本小题满分8分）
为了了解某市在减轻学生作业负担的工作上的落实情况，该市教育局对某校某班每个同学晚上完成作业的时间进行了一次调查统计，并根据收集的数据绘制了如图所示的两幅不完整的统计图，请你根据图中提供的信息，完成下面的问题
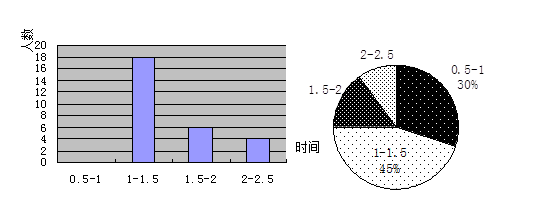
1.（1）该班共有多少学生？
2.（2）将图中的条形统计图补充完整
3.（3）求作业完成时间在0.5-1小时的部分对应扇形圆心角是多少度？
4.（4）如果该校七年级共有1000名学生，请估计七年级学生完成作业时间超过1.5小时的大约有多少人？
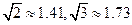） （本小题满分8分）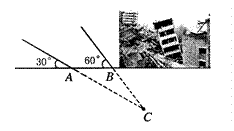
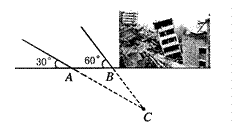
2011年3月10日，云南盈江县发生里氏5．8级地震。萧山金利浦地震救援队接到上级命令后立即赶赴震区进行救援。救援队利用生命探测仪在某建筑物废墟下方探测到点 C 处有生命迹象，已知废墟一侧地面上两探测点A、B 相距3米，探测线与地面的夹角分别是30°和 60°（如图），试确定生命所在点 C 的深度。（结果精确到0.1米，参考数据：
）
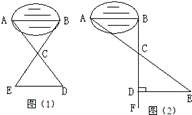
（本小题满分12分）某班同学到野外活动，为测量一池塘两端A、B的距离，设计了几种方案，下面介绍两种：（I）如图（1），先在平地取一个可以直接到达A、B的点C，并分别延长AC到D，BC到E，使DC=AC，BC=EC，最后测出DE的距离即为AB的长。（II）如图（2），先过B点作AB的垂线BF，再在BF上取C、D两点，使BC=CD，接着过点D作BD的垂线DE，交AC的延长线于E，则测出DE的长即为AB的距离。阅读后回答下列问题：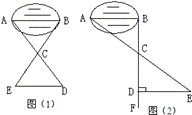
【小题1】（1）方案（I）是否可行？为什么？
【小题2】（2）方案（II）是否切实可行？为什么？
【小题3】（3）方案（II）中作BF⊥AB，ED⊥BF的目的是 ；若仅满足∠ABD=∠BDE≠90°，方案（II）是否成立？
【小题4】（4）方案（II）中，若使BC=n·CD，能否测得（或求出）AB的长？理由是 ，若ED=m，则AB= 。
一．1．C； 2．C； 3.C； 4．B； 5．Ｄ； 6．B； 7．A； 8．B； 9．A； 10．C。
二．11．x≥2； 12．1； 13．25°； １４．１４５； １５．１６；
１６．１８０； １７．①，③； １８．
三．１９解：原式
?????????????????????????????????????????????????????????????????????????? 2分
???????????????????????????????????????????????????????????????????????????????????????????? ５分
当
时，原式
．??????????????????????????????????????????????????????? ７分．
２０．解：（1）
（名），
本次调查了90名学生．?????????????????????????????????????????????????????????????????????????????????????? （2分）
补全的条形统计图如下：
    （名），
（3）略（语言表述积极进取，健康向上即可得分）．?????????????????????????????????????????????? （7分） ２１．(本题满分８分) 解：（1）如图，由题意得，∠EAD=45°，∠FBD=30°． ∴ ∠EAC=∠EAD+∠DAC =45°+15°=60°． ∵ AE∥BF∥CD， ∴ ∠FBC=∠EAC=60°． ∴ ∠DBC=30°． ???????????????????????????????????????? 2分 又∵ ∠DBC=∠DAB+∠ADB， ∴ ∠ADB=15°． ∴ ∠DAB=∠ADB． ∴ BD=AB=2． 即B，D之间的距离为 （2）过B作BO⊥DC，交其延长线于点O， 在Rt△DBO中，BD=2，∠DBO=60°． ∴ DO=2×sin60°=2× 在Rt△CBO中，∠CBO=30°，CO=BOtan30°= ∴ CD=DO－CO= 即C，D之间的距离为
２２．解：（1） （2）290，甲，20．????????????????????????????????????????????????????????????????????????????????? 6分（每空1分） （3）在5月17日，甲厂生产帐篷50顶，乙厂生产帐篷30顶．???????????????????????????????????? 6分 设乙厂每天生产帐篷的数量提高了
答：乙厂每天生产帐篷的数量提高了
２３．解：（1）① 等边三角形；②重叠三角形 （2）用含
（3）能；t=2。．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．１０分． ２４．本小题满分1０分． （Ⅰ）证明 将△ 则△
又由 由
得 又 ∴△ 有 ∴ ∴在Rt△ 得 （Ⅱ）关系式
则△ 有
又由 由
得 又 ∴△ 有 ∴ ∴在Rt△ 得 （３）．能；在直线ＡＢ上取点Ｍ，Ｎ使∠ＭＣＮ＝４５°．．．．．．．．．．．．．．．．．．．．．．１０分 ２５．（本题满分12分） 解：（1）设正方形的边长为
即 解得
（注：通过观察、验证直接写出正确结果给3分） （2）有侧面积最大的情况． 设正方形的边长为 则
即 改写为
即当剪去的正方形的边长为2.25cm时，长方体盒子的侧面积最大为40.5cm2．?????????????? 7分
设正方形的边长为 若按图1所示的方法剪折，则
即
若按图2所示的方法剪折，则
即
比较以上两种剪折方法可以看出，按图2所示的方法剪折得到的盒子侧面积最大，即当剪去的正方形的边长为 说明：解答题各小题只给了一种解答及评分说明，其他解法只要步骤合理，解答正确，均应给出相应分数． ２６．（本小题满分12分） 解：（1）在Rt△ABC中， 由题意知：AP = 5－t，AQ = 2t， 若PQ∥BC，则△APQ ∽△ABC， ∴ ∴
（2）过点P作PH⊥AC于H． ∵△APH ∽△ABC， ∴ ∴ ∴ ∴ （3）若PQ把△ABC周长平分， 则AP+AQ=BP+BC+CQ． ∴ 解得： 若PQ把△ABC面积平分， 则 ∵ t=1代入上面方程不成立， ∴不存在这一时刻t，使线段PQ把Rt△ACB的周长和面积同时平分．???????????????? 9′ （4）过点P作PM⊥AC于Ｍ，PN⊥BC于N，
∵PM⊥AC于M， ∴QM=CM． ∵PN⊥BC于N，易知△PBN∽△ABC． ∴ ∴ ∴ ∴ 解得： ∴当 此时 在Rt△PMC中， ∴菱形PQP ′ C边长为
同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com版权声明：本站所有文章，图片来源于网络，著作权及版权归原作者所有，转载无意侵犯版权，如有侵权，请作者速来函告知，我们将尽快处理，联系qq：3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |
,BO=2×cos60°=1．??????????????????????????????????????????????????? ６分
，
（km）．
km． ????????????????????????????????????????????????????????????????????????? ８分
，则
?????????????????????????????????????? 7分
．
．?????????????????????????????????????????????????????????????????? 8分
的面积为
．?????????????????????????? 5分
的代数式表示重叠三角形
；?????????????????????????? 7分
．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．8分
沿直线
对折，得△
，连
，
有
，
，
，
．
，得 
． ????????????????????????????????????????? 2分
，
，
． ??????????????????????????????????????????????????????????????????????????????????????????????????? 3分
，
≌△
． ???????????????????????????????????????????????????????????????????????????????????????????? 4分
，
．
．???????????????????????????????????????????????????????????? ５分
中，由勾股定理，
．即
． ??????????????????????????????????????????????????????? ６分
证明 将△
，连
，
，
，
，
．
．
，
．
． ??????????????????????????????????????????????????????????????????????????????????????????????? ８分
≌△
，
，
，
． 
中，由勾股定理，
．即
cm，则
．?????????????????????????????????????????????????????????????????????????????????????????????? 1分
．
（不合题意，舍去），
．
cm2，
．
．????????????????????????????????????????????????????????????????????????????????????????????????????? 5分
．
时，
．
（3）有侧面积最大的情况．
．
．
时，
．??????????????????????????????????? 9分
．
．
时，
．??????????????????????????????????????????????????????????????????????????????????????? 11分
cm时，折成的有盖长方体盒子的侧面积最大，最大面积为
cm2．
，
，
，
∴
．
??????????????????????????????????????????????????????? 3′
，
，
，
． ??????????????????????????????????????????? 6′
， 
．
， 即－
＋3t=3．
若四边形PQP ′ C是菱形，那么PQ＝PC．
， ∴
，
， 
，
，
．
， 
，
，
．?????????????????????????????????????????????????????????????????????????? 12′