
题目列表(包括答案和解析)
 (2012•江苏一模)本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
(2012•江苏一模)本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.已知抛物线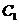 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线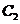 :
: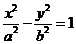 的一个焦点
的一个焦点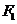 且垂直于
且垂直于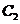 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线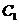 与双曲线
与双曲线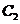 的一个交点是
的一个交点是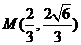 .
.
(Ⅰ)求抛物线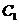 的方程及其焦点
的方程及其焦点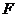 的坐标;
(Ⅱ)求双曲线
的坐标;
(Ⅱ)求双曲线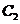 的方程及其离心率
的方程及其离心率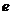 .
.
【解析】本试题主要考查了抛物线方程的求解,以及双曲线与抛物线的交点问题,和双曲线的几何性质的综合求解和运用。

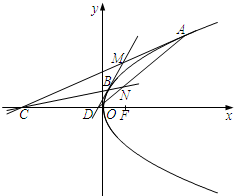 本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.
本题主要考查抛物线的标准方程、简单的几何性质等基础知识,考查运算求解、推理论证的能力.已知抛物线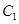 的顶点在坐标原点,它的准线经过双曲线
的顶点在坐标原点,它的准线经过双曲线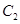 :
: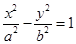 的一个焦点
的一个焦点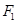 且垂直于
且垂直于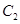 的两个焦点所在的轴,若抛物线
的两个焦点所在的轴,若抛物线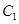 与双曲线
与双曲线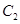 的一个交点是
的一个交点是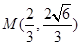 .
.
(Ⅰ)求抛物线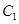 的方程及其焦点
的方程及其焦点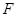 的坐标;
(Ⅱ)求双曲线
的坐标;
(Ⅱ)求双曲线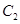 的方程及其离心率
的方程及其离心率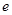 .
.
【解析】本试题主要考查了抛物线方程的求解,以及双曲线与抛物线的交点问题,和双曲线的几何性质的综合求解和运用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com