
题目列表(包括答案和解析)
| f(x1)+f(x2) |
| 2 |
| x1+x2 |
| 2 |
| 1 |
| x |
| 1 |
| x |
若在上凸函数f(x)的图象上依次取n个(n≥3)点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),则凸n边到P1P2P3…Pn的生心G(![]() ,
,![]() )必在函数y=f(x)的图象下方或图象上。
)必在函数y=f(x)的图象下方或图象上。
运用上述定义或性质证明。
(1)f(x)=lgx在区间(0,+∞)上是上凸函数;
(2)设x1,x2,…,xn为正实数,则![]() ≥
≥![]() 。
。
定义:若对于给定区间D内任意的实数x1和x2都有f(![]() )≥
)≥![]() [f(x1)+f(x2)],则称函数f(x)是区间D上的上凸函数。上凸函数有如下的性质:
[f(x1)+f(x2)],则称函数f(x)是区间D上的上凸函数。上凸函数有如下的性质:
若在上凸函数f(x)的图象上依次取n个(n≥3)点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),则凸n边到P1P2P3…Pn的生心G(![]() ,
,![]() )必在函数y=f(x)的图象下方或图象上。
)必在函数y=f(x)的图象下方或图象上。
运用上述定义或性质证明。
(1)f(x)=lgx在区间(0,+∞)上是上凸函数;
(2)设x1,x2,…,xn为正实数,则![]() ≥
≥![]() 。
。
| 1 |
| x |
| x2-1 |
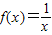 ,②f(x)=sinx,③
,②f(x)=sinx,③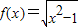 ,其中在区间[1,+∞)上通道宽度可以为1的函数有( )
,其中在区间[1,+∞)上通道宽度可以为1的函数有( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com