
题目列表(包括答案和解析)
| v | 2 0 |
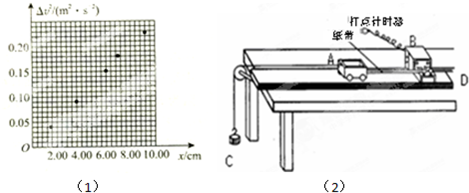
某同学探究恒力做功和物体动能变化间的关系,方案如图所示.
(1)为消除摩擦力对实验的影响,可以使木板适当倾斜以平衡摩擦阻力,则在不挂钩码的情况下,下面操作正确的是
A.未连接纸带前,放开小车,小车能由静止开始沿木板下滑
B.未连接纸带前,轻碰小车,小车能匀速稳定下滑
C.放开拖着纸带的小车,小车能由静止开始沿木板下滑
D.放开拖着纸带的小车,轻碰小车,小车能匀速稳定下滑
(2)平衡摩擦力后,他想用钩码的重力表示小车受到的合外力,则实验中应满足:
(3)该同学在一条比较理想的纸带上,从点迹清晰的某点开始记为O点,顺次选取5个点,分别测量这5个点到O点之间的距离x,计算出它们与O点之间的速度平方差![]() ,然后在坐标纸上建立
,然后在坐标纸上建立![]() 坐标系,并根据上述数据进行如图所示的描点,请画出
坐标系,并根据上述数据进行如图所示的描点,请画出![]() 变化图像。
变化图像。
(4) 若测出小车质量为0.2kg,悬挂钩码质量为0.026kg,g=10m/s2,由![]() 变化图像,取x=6.00cm,小车动能增量为 J,恒力做功为 J,在误差允许范围内可认为二者相等。(保留三位有效数字)
变化图像,取x=6.00cm,小车动能增量为 J,恒力做功为 J,在误差允许范围内可认为二者相等。(保留三位有效数字)
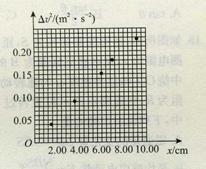
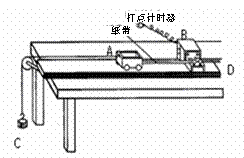
某同学探究恒力做功和物体动能变化间的关系,方案如图所示.
(1)为消除摩擦力对实验的影响,可以使木板适当倾斜以平衡摩擦阻力,则在不挂钩码的情况下,下面操作正确的是
A.未连接纸带前,放开小车,小车能由静止开始
沿木板下滑
B.未连接纸带前,轻碰小车,小车能匀速稳定下滑
C.放开拖着纸带的小车,小车能由静止开始沿木板下滑
D.放开拖着纸带的小车,轻碰小车,小车能匀速稳定下滑
(2)平衡摩擦力后,他想用钩码的重力表示小车受到的合外力,
则实验中应满足:
(3)该同学在一条比较理想的纸带上,从点迹清晰的某点开始记为O点,顺次选取5个点,分别测量这5个点到O点之间的距离x,计算出它们与O点之间的速度平方差![]() ,然后在坐标纸上建立
,然后在坐标纸上建立![]() 坐标系,并根据上述数据进行如图所示的描点,请画出
坐标系,并根据上述数据进行如图所示的描点,请画出![]() 变化图像。
变化图像。
(4) 若测出小车质量为0.2kg,悬挂钩码质量为0.026kg,g=10m/s2,由![]() 变化图像,取x=6.00cm,小车动能增量为 J,恒力做功为 J,在误差允许范围内可认为二者相等。(保留三位有效数字)
变化图像,取x=6.00cm,小车动能增量为 J,恒力做功为 J,在误差允许范围内可认为二者相等。(保留三位有效数字)



| 实验次数 | 橡皮筋根数 | 速度(m/s) |
| 1 | 1 | 1.00 |
| 2 | 2 | 1.40 |
| 3 | 3 | 1.75 |
| 4 | 4 | 2.00 |
| 5 | 5 | 2.20 |
| 6 | 6 | 2.48 |
某课外兴趣小组在研究“恒力做功和物体动能变化之间的关系”的实验中使用了如右图所示的实验装置:
(1)该小组同学实验时在安装正确,操作规范的前提下(已平衡摩擦力),用钩码的重力表示小车受到的合外力,为减小由此带来的系统误差,钩码的质量m和小车的总质量M之间需满足的条件是:M ▲ m;
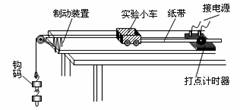 (2)实验时,小车由静止开始释放,已知释放时钩码底端离地高度为H,现测出的物理量还有:小车由静止开始起发生的位移s(s<H)、小车发生位移s时的速度大小为v,钩码的质量为m,小车的总质量为M,设重力加速度为g,则实际测量出的合外力的功mgs将 ▲ (选填“大于”、 “小于”或“等于”)小车动能的变化;若用该实验装置验证系统机械能守恒定律,即需验证关系式 ▲ 成立;
(2)实验时,小车由静止开始释放,已知释放时钩码底端离地高度为H,现测出的物理量还有:小车由静止开始起发生的位移s(s<H)、小车发生位移s时的速度大小为v,钩码的质量为m,小车的总质量为M,设重力加速度为g,则实际测量出的合外力的功mgs将 ▲ (选填“大于”、 “小于”或“等于”)小车动能的变化;若用该实验装置验证系统机械能守恒定律,即需验证关系式 ▲ 成立;
(3)在上述实验中打点计时器使用的交流电频率为50Hz,实验中某段纸带的打点记录如图所示,则小车运动的加速度大小为 ▲ m/s2(保留3位有效数字).
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com