练习册

  • 练习册
  • 试题
    3．空间图形是由点.线.面组成的点.线.面的基本位置关系如下表所示: 图形 符号语言 文字语言 图形 符号语言 文字语言 点在直线上 直线在平面内 点不在直线上 直线与平面无公共点 点在平面内 直线与平面交于点 点不在平面内 直线.交于点 平面.相交于直线 (平面外的直线)表示()或 4平面的基本性质 公理1 如果一条直线的两点在一个平面内.那么这条直线上的所有点都在这个平面内 推理模式:． 如图示: 应用:是判定直线是否在平面内的依据.也可用于验证一个面是否是平面． 公理1说明了平面与曲面的本质区别．通过直线的“直 来刻划平面的“平 .通过直线的“无限延伸 来描述平面的“无限延展性 .它既是判断直线在平面内.又是检验平面的方法． 公理2如果两个平面有一个公共点,那么它们还有其他公共点,且所有这些公共点的集合是一条过这个公共点的直线 推理模式:且且唯一如图示: 应用:①确定两相交平面的交线位置,②判定点在直线上 公理2揭示了两个平面相交的主要特征.是判定两平面相交的依据.提供了确定两个平面交线的方法． 公理3 经过不在同一条直线上的三点.有且只有一个平面 推理模式:不共线存在唯一的平面.使得 应用:①确定平面,②证明两个平面重合 “有且只有一个 的含义分两部分理解.“有 说明图形存在.但不唯一.“只有一个 说明图形如果有顶多只有一个.但不保证符合条件的图形存在.“有且只有一个 既保证了图形的存在性.又保证了图形的唯一性．在数学语言的叙述中.“确定一个 .“可以作且只能作一个 与“有且只有一个 是同义词.因此.在证明有关这类语句的命题时.要从“存在性 和“唯一性 两方面来论证． 5平面图形与空间图形的概念:如果一个图形的所有点都在同一个平面内.则称这个图形为平面图形.否则称为空间图形 6公理的推论: 推论1 经过一条直线和直线外的一点有且只有一个平面. 推理模式:存在唯一的平面.使得. 推论2 经过两条相交直线有且只有一个平面 推理模式:存在唯一的平面.使得 推论3 经过两条平行直线有且只有一个平面 推理模式:存在唯一的平面.使得 【查看更多】

     

    题目列表(包括答案和解析)

    如图，ABCD是边长为2的正方形纸片，沿某动直线l为折痕将正方形在其下方的部分向上翻折，使得每次翻折后点B都落在边AD上，记为B'；折痕与AB交于点E，以EB和EB’为邻边作平行四边形EB’MB．若以B为原点，BC所在直线为x轴建立直角坐标系（如下图）：
    （Ⅰ）．求点M的轨迹方程；
    （Ⅱ）．若曲线S是由点M的轨迹及其关于边AB对称的曲线组成的，等腰梯形A1B1C1D1的三边A1B1，B1C1，C1D1分别与曲线S切于点P，Q，R．求梯形A1B1C1D1面积的最小值．

    查看答案和解析>>

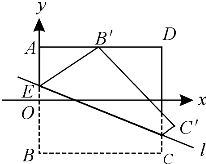    精英家教网如图，ABCD是边长为2的正方形纸片，沿某动直线l为折痕，正方形在其下方的部分向上翻折，使得每次翻折后点B都落在边AD上，记为B′；折痕l与AB交于点E，点M满足关系式
    EM
    =
    EB
    +
    EB′
    ．
    （1）如图，建立以AB中点为原点的直角坐标系，求点M的轨迹方程；
    （2）若曲线C是由点M的轨迹及其关于边AB对称的曲线组成的，
    F是AB边上的一点，
    BA
    BF
    =4，过点F的直线交曲线C于P、Q两点，且
    PF
    =λ
    FQ
    ，求实数λ的取值范围．

    查看答案和解析>>

    PA,PB,PC是由点P出发的三条射线,两两夹角为60°,则PC与它在平面PAB内的射影所成角的余弦值为（    ）

    A.           B.             C.             D.

    查看答案和解析>>

    已知a=(-1,2),

    (1)把点A(3，4)按a平移，求对应点A′的坐标(x′,y′)；

    (2)若点N(3，4)是由点M按a平移得到的，求M点的坐标.

    查看答案和解析>>

    如图，ABCD是边长为2的正方形纸片，沿某动直线为折痕将正方形在其下方的部分向上翻折，使得每次翻折后点B都落在边AD上，记为；折痕与AB交于点E，以EB和EB’为邻边作平行四边形EB’MB。若以B为原点，BC所在直线为x轴建立直角坐标系（如下图）：

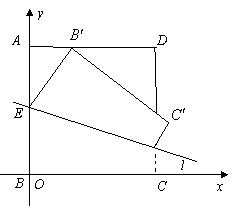    （Ⅰ）．求点M的轨迹方程；

    （Ⅱ）．若曲线S是由点M的轨迹及其关于边AB对称的曲线组成的，等腰梯形的三边分别与曲线S切于点.求梯形面积的最小值.


                

    查看答案和解析>>


    同步练习册答案