练习册

  • 练习册
  • 试题
    我们知道.物体作匀速直线运动的位移s是时间t的函数.即s=vt,其中速度v是常量,定义域t 0,值域s 0,反过来.也可以由位移s和速度v确定物体作匀速直线运动的时间.即.这时.位移s是自变量.时间t是位移s的函数,定义域s 0,值域t 0. 又如.在函数中.x是自变量.y是x的函数.定义域xR.值域yR. 我们从函数中解出x.就可以得到式子. 这样.对于y在R中任何一个值.通过式子.x在R中都有唯一的值和它对应. 因此.它也确定了一个函数:y为自变量.x为y的函数.定义域是yR.值域是xR. 综合上述.我们由函数s=vt得出了函数,由函数得出了函数.不难看出.这两对函数中.每一对中两函数之间都存在着必然的联系:①它们的对应法则是互逆的,②它们的定义域和值域相反:即前者的值域是后者的定义域.而前者的定义域是后者的值域. 我们称这样的每一对函数是互为反函数. 【查看更多】

     

    题目列表(包括答案和解析)

    下列事件中,是随机事件的有(　　)

    ①函数y=logax(a>0且a≠1)在定义域上是增函数　②某人打开邮箱,恰好有新邮件　③自由下落的物体作匀速直线运动　④盒子中有5个白球,2个红球,从中任取3个球,则至少有1个白球

    　　　　　　　　　　　　　

    A.①②     B.①③      C.②③    D.③④

    查看答案和解析>>

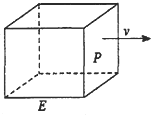    如图，长方形物体E在雨中沿面P（面积为S）的垂直方向作匀速移动，速度为v（v＞0），物体E移动时单位时间内的淋雨量包括两部分：
    ①P或P的平行面（只有一个面淋雨）的淋雨量，设其值与|v-4|×S成正比，比例系数为
    1
    10
    ；
    ②其它面的淋雨量之和，其值为
    1
    2
    ，记y为物体E移动过程中的总淋雨量，当移动距离d=100，面积S=
    3
    2
    时．
    （Ⅰ）写出y的表达式；
    （Ⅱ）设0＜v≤10，试确定移动速度v，使总淋雨量y最少．

    查看答案和解析>>

    （2010•台州二模）在O点测量到远处有一物体在作匀速直线运动，开始时该物体位于P点，一分钟后，其位置在Q点，且∠POQ=
    π
    2
    ，再过一分钟后，该物体位于R点，且∠QOR=
    π
    6
    ，则tan∠OPQ等于（　　）

    查看答案和解析>>

    19、我们知道，如果集合A⊆S，那么S的子集A的补集为CSA={x|x∈S，且x∉A}．类似地，对于集合A、B，我们把集合{x|x∈A，且x∉B}叫做集合A与B的差集，记作A-B．
    据此回答下列问题：
    （1）若A={1，2，3，4}，B={3，4，5，6}，求A-B；
    （2）在下列各图中用阴影表示集合A-B．

    查看答案和解析>>

    （2012•静安区一模）我们知道，当两个矩阵P、Q的行数与列数分别相等时，将它们对应位置上的元素相减，所得到的矩阵称为矩阵P与Q的差，记作
    P-Q．已知矩阵P=
    cosA•sinAosA
    16tanBcosA
    ，Q=
    1sinA
    12-sinA
    ，M=
    -
    109
    169
    		-a2
    0
    17
    13
    ，满足P-Q=M．求下列三角比的值：
    （1）sinA，cosA；
    （2）sin（A-B）．

    查看答案和解析>>


    同步练习册答案