
题目列表(包括答案和解析)
| 25 | 28 |
| 2 |
| 3 |
| 3 |
| 5 |
某学校为了增强学生对消防安全知识的了解,举行了一次消防安全知识竞赛.其中一道题是连线题,要求将3种不同的消防工具与它们的用途一对一连线,规定:每连对一条得2分,连错一条扣1分,参赛者必须把消防工具与用途一对一全部连起来.
(Ⅰ)设三种消防工具分别为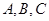 ,其用途分别为
,其用途分别为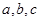 ,若把
,若把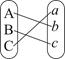 连线方式表示为
连线方式表示为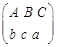 ,规定第一行
,规定第一行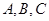 的顺序固定不变,请列出所有连线的情况;
的顺序固定不变,请列出所有连线的情况;
(Ⅱ)求某参赛者得分为0分的概率.
某学校为了增强学生对消防安全知识的了解,举行了一次消防安全知识竞赛.其中一道题是连线题,要求将3种不同的消防工具与它们的用途一对一连线,规定:每连对一条得2分,连错一条扣1分,参赛者必须把消防工具与用途一对一全部连起来.
(Ⅰ)设三种消防工具分别为 ,其用途分别为
,其用途分别为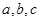 ,若把
,若把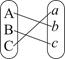 连线方式表示为
连线方式表示为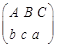 ,规定第一行
,规定第一行 的顺序固定不变,请列出所有连线的情况;
的顺序固定不变,请列出所有连线的情况;
(Ⅱ)求某参赛者得分为0分的概率.
(本题满分13分)
甲、乙两人同时参加某电台举办的有奖知识问答。约定甲,乙两人分别回答4个问题,答对一题得1分,不答或答错得0分,4个问题结束后以总分决定胜负。甲,乙回答正确的概率分别是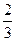 和
和 ,且不相互影响。求:
,且不相互影响。求:
(1) 甲回答4次,至少得1分的概率;
(2) 甲恰好以3分的优势取胜的概率。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com