
题目列表(包括答案和解析)
已知关于 的方程
的方程 ,下列说法正确的是
,下列说法正确的是
A.当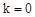 时,方程无解
时,方程无解
B.当 时,方程有一个实数解
时,方程有一个实数解
C.当 时,方程有两个相等的实数解
时,方程有两个相等的实数解
D.当 时,方程总有两个不相等的实数解
时,方程总有两个不相等的实数解
已知关于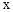 的方程
的方程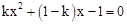 ,下列说法正确的是
,下列说法正确的是
A.当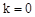 时,方程无解 时,方程无解 |
B.当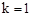 时,方程有一个实数解 时,方程有一个实数解 |
C.当 时,方程有两个相等的实数解 时,方程有两个相等的实数解 |
D.当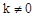 时,方程总有两个不相等的实数解 时,方程总有两个不相等的实数解 |
已知关于![]() 的方程
的方程![]() ,下列说法正确的是( ).
,下列说法正确的是( ).
A.当![]() 时,方程无解
时,方程无解
B.当![]() 时,方程有一个实数解
时,方程有一个实数解
C.当![]() 时,方程有两个相等的实数解
时,方程有两个相等的实数解
D.当![]() 时,方程总有两个不相等的实数解
时,方程总有两个不相等的实数解
 .解:当
.解:当 时,原方程可化为
时,原方程可化为 ,解得
,解得 ;当
;当 时,原方程可化为
时,原方程可化为 ,解得
,解得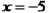 .所以原方程的解是
.所以原方程的解是 或
或

 为何值时,关于
为何值时,关于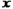 的方程
的方程 ⑴无解;⑵只有一个解;⑶有两个解
⑴无解;⑵只有一个解;⑶有两个解阅读下列材料:
解方程![]() .
.
解:方程的两边都乘以![]() ,约去分母,得
,约去分母,得![]() .
.
解这个整式方程,得![]() .
.
检验:当![]() 时,
时,![]() ,所以2是增根,原方程无解.
,所以2是增根,原方程无解.
请你根据这个方程的特点,用另一种方法解这个方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com