实验室有一个用铜漆包线绕在铁芯上制成的电感线圈（线圈与铁芯不能拆分），从剩余材料可知漆包线粗细均匀，横截面呈圆形，该电感线圈的直流电阻约为5Ω，允许通过最大电流为3A，查得铜的电阻率为ρ，密度为ρ₀．
请设计一个实验方案，不拆线圈、间接测出线圈所用的漆包线的总长度．现有以下实验器材供选择：
 A．螺旋测微器           
B．刻度尺                  
C．电流表A（量程为0.6A，内阻约为0.5Ω）
D．定值电阻R₀ = 9900Ω
E．电流计G（满偏电流I_g = 300μA，准确的内阻值R_g = 100Ω）
F．滑动变阻器R₁ (20Ω，3A)
G．滑动变阻器R ₂ (2KΩ，3A)
H．蓄电池E （电动势6V，内阻约为0.01Ω）
I．开关、导线若干．
（1）根据你的设计方案，除被测电感线圈外，选用的实验器
材有__________（填字母代号）
（2）在方框中画出你所设计的实验电路图，标明所用器材的符号．
（3）实验中需要直接测量的物理量及对应字母是                                 
（4）若只测量一次，请写出漆包线总长度的表达式L  = __________________________．
（用字母表示，不写具体数值）
.

查看答案和解析>>

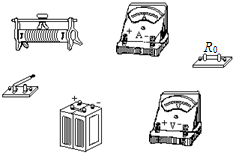图为用伏安法测量一个直流毫安表A内阻的实验 所需的器材实物图，器材规格如下：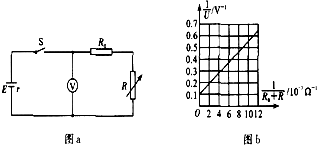
A．定值保护电阻R₀（约250Ω）
B．待测直流毫安表A（量程0～10mA，内阻约100Ω）
C．直流电压表（量程0～2V，内阻约5kΩ）
D．直流电源（输出电压4V，内阻可不计）
E．滑动变阻器（阻值范围0～15Ω，允许最大电流1A）
F．电健一个，导线若干条．
（1）根据器材的规格和实验要求，画出测量电路原理图．
（2）根据你画的测量电路原理图在本题的实物图上连线．

查看答案和解析>>

现有一种特殊的电池，它的电动势E约为9V，内阻r约为50Ω，已知该电池允许输出的最大电流为50mA．为了测定这个电池的电动势和内阻，某同学利用如图a所示的电路进行实验．图中电压表的内阻很大，对电路的影响可不考虑，R为电阻箱，阻值范围0～9999Ω，R₀是定值电阻，起保护电路的作用．
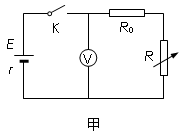
（1）实验室备有的定值电阻有以下几种规格：
A．10Ω，2.5W     B．100Ω，1．OW    C．200Ω，1．OW    D.2000Ω，5.0W
本实验应选哪一种规格？
答：

C

C

（只需填规格的代号）．

（2）该同学接入符合要求的R₀后，闭合开关S，调整电阻箱的阻值，读取电压表的示数，改变电阻箱阻值，取得多组数据，作出了如图b所示的图线．则根据该同学所作出的图线可求得该电池的电动势E为

10

10

V，内阻r为

46

46

Ω．
（3）现有一阻值为10.0Ω的定值电阻、一个电键、若干根导线和一个电压表，该电压表表面上有刻度但无刻度值，请设计一个能粗略测定上述电源的电动势和内阻的实验方案．（已知电压表内阻很大，电压表量程大于电源电动势）要求：
①画出实验电路图；
②简要写出完成接线后的实验步骤；
③写出用测得的量计算电源内阻的表达式．

查看答案和解析>>

查看答案和解析>>

查看答案和解析>>

（物理部分）

第Ⅰ卷

 二、选择题（48分）

14．A  15．C  16．B  17．B  18．AD  19．CD  20．AD   21．C

第Ⅱ卷

22．（17分）

  （1）0.949或0.950             （2分）

  （2）①1.94  1.94   9.7  ②受到（每空2分，共8分）

（3）①见图  评分标准：测量电路正确2分，变阻器接法正确2分，全对得4分

②80±2Ω

23．（16分）

解：（1）设该队员下滑中的最大速度为v，滑至地面前瞬间的速度为v₁，做匀减速直线运动的加速度为a，在整段过程中运动的时间分别为t₁和t₂，下滑的距离分别为h₁和h₂

该队员先做自由落体运动，有 v²＝2gh₁              ①               （1分）

    接着做匀减速直线运动，有   v²－v₁²＝2ah₂           ②               （1分）

f_max－_mg＝ma                                     ③              （2分）

且 s＝h₁＋h₂                                      ④              （1分）

      v₁＝6m/s

由③式得：a＝5m/s²                                               （1分）

再由①②④式联立可得  v＝10m/s                                  （2分）

所以该队员下滑过程中动量的最大值p＝mv＝650kg?m/s              （2分）

（2）由v＝gt₁                               ⑤                  （1分）

  v－v₁＝at₂                                 ⑥                  （1分）

由⑤⑥式可得  t₁＝1s   t₂＝0.8s                                       （2分）

所以该队员下滑过程的最短时间t＝t₁＋t₂＝1.8 s                          （2分）

24．（19分）

解：（1）设子弹射入物块前的速度大小为v₀，射入后共同速度的大小为v，

子弹击中乙的过程中动量守恒，有 mv₀＝（m＋m_乙）v     ①         （3分）

乙上摆到最高点的过程，机械能守恒

有                   ②           （3分）

联立②③解得 v₀＝300m/s                                          （2分）

（2）设甲物体的质量为m_甲，说受的最大静摩擦力为f，斜面的倾角为θ，

当乙物体运动到最高点时，绳子上的弹力设为T₁，

         T₁＝（m＋m_乙）gcosθ                         ③          （2分）

此时甲物体恰好不下滑，有 m_甲g sinθ＝f＋T₁           ④         （2分）

当乙物体运动到最低点时，绳子上的弹力设为T₂，

由牛顿第二定律：           ⑤         （2分）

此时甲物体恰好不上滑，有 m_甲g sinθ＋f＝T₂            ⑥       （2分）

联立②③④⑤⑥解得 N               （3分）

25．（20分）

解：（1）带电系统锁定解除后，在水平方向上受到向右的电场力作用开始向右加速运动，当B进入电场区时，系统所受的电场力为A、B的合力，因方向向左，从而做减速运动，以后不管B有没有离开右边界，速度大小均比B刚进入时小，故在B刚进入电场时，系统具有最大速度。

设B进入电场前的过程中，系统的加速度为a₁，由牛顿第二定律：

2Eq＝2ma₁                                           （2分）

B刚进入电场时，系统的速度为v_m，由 可得      （3分）

（2）对带电系统进行分析，假设A能达到右边界，电场力对系统做功为W₁

则                                     （2分）

故系统不能从右端滑出，即：当A刚滑到右边界时，速度刚好为零，接着反向向左加速。由运动的对称性可知，系统刚好能够回到原位置，此后系统又重复开始上述运动。 

（2分）

     设B从静止到刚进入电场的时间为t₁，则              （1分）

设B进入电场后，系统的加速度为a₂，由牛顿第二定律（1分）

显然，系统做匀减速运动，减速所需时间为t₂，则有  （1分）

那么系统从开始运动到回到原出发点所需的时间为   （2分）

（3）当带电系统速度第一次为零，即A恰好到达右边界NQ时，B克服电场力做的功最多，B增加的电势能最多，此时B的位置在PQ的中点处                 （1分）

所以B电势能增加的最大值                   （3分）